位运算

位运算就是基于整数的二进制进行的运算。由于计算机内部就是以二进制来存储数据，位运算是相当快的。

基本的位运算共 6 种：有与、或、非、异或、左移、右移运算。

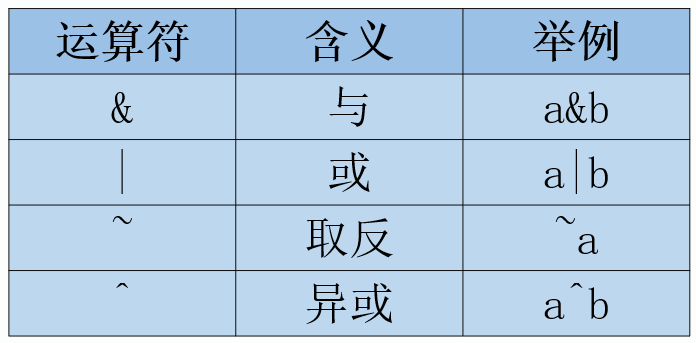
位逻辑运算符

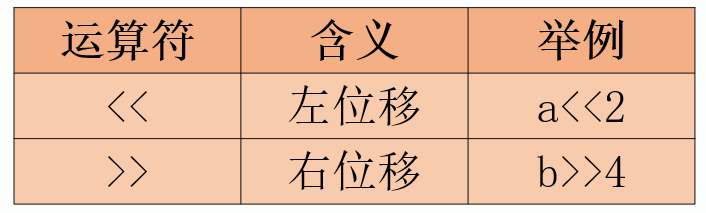
位移运算符

与运算(&)：按位进行“与”运算，两数同一位都为1时结果为1，否则为0。例如:101&110=100。

或运算(|)：按位进行“或”运算，两数同一位都为0时结果为0，否则为1。例如:101|110=111。

非运算(~)：按位取反。例如~101=010。

“异或”（^） 它的规则是：若参加运算的两个二进制位值相同则为0，否则为1.

异或运算有一个特别重要的性质：a^a=0

此外，异或运算是满足交换律和结合律的，有a ^ b ^b=a ^ 0=a

左移(<<)：左移一位，相当于某数乘以2，比如110左移1位变为1100 ，右边的空位补0，6变为12，表示为(110<<1) 因此左移$x$位，相当于该数乘以$2^x$

右移(>>)：右移一位，相当于某数除以2，比如110右移1位变为011，6变为3，表示为(110>>1) 因此右移$x$位，相当于该数除以$2^x$。

位运算的应用

位运算一般有三种作用：

1. 高效地进行某些运算，代替其它低效的方式。
2. 表示集合（常用于 状压 DP）。
3. 题目本来就要求进行位运算。

需要注意的是，用位运算代替其它运算方式（即第一种应用）在很多时候并不能带来太大的优化，反而会使代码变得复杂，使用时需要斟酌。（但像「乘 2 的非负整数次幂」和「除以 2 的非负整数次幂」就最好使用位运算，因为此时使用位运算可以优化复杂度。）

有关 2 的幂的应用

由于位运算针对的是变量的二进制位，因此可以推广出许多与 2 的整数次幂有关的应用。

将一个数乘（除） 2 的非负整数次幂：

int mul(int n, int m) {  // 计算 n*(2^m)
  return n << m;
}
int div(int n, int m) {  // 计算 n/(2^m)
  return n >> m;
}

快速幂

long long binpow(long long a, long long b) {
  long long res = 1;
  while (b > 0) {
    if (b & 1) res = res * a;
    a = a * a;
    b >>= 1;
  }
  return res;
}

操作一个数的二进制位

获取一个数二进制的某一位：

// 获取 a 的第 b 位，最低位编号为 0
int getBit(int a, int b) { return (a >> b) & 1; }

将一个数二进制的某一位设置为 0：

// 将 a 的第 b 位设置为 0 ，最低位编号为 0
int unsetBit(int a, int b) { return a & ~(1 << b); }