什么是幂

通常幂指的是一个数自己乘自己若干次的形式。

字面意思

“幂”原指覆盖东西的布。

数学意思

求几个相同因数的积的运算，叫做乘方。乘方的结果叫做幂。（$a^n$）

$a^n$ = a × a × a × … × a，这里有 n 个 a 相乘。并且我们称 $a^n$ 当中 a 为底数、n 为指数， $a^n$ 为 a 的 n 次方或者 n 次幂。

举例子：

$2^3$ = 2 × 2 × 2， 这里底数 a 是 2，指数 n 是 3

$2^4$ = 2 × 2 × 2 × 2， 这里底数 a 是 2，指数 n 是 4

幂的 4 种运算

1、同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加 $a^m$ x $a^n$ = $a^{m+n}$

​

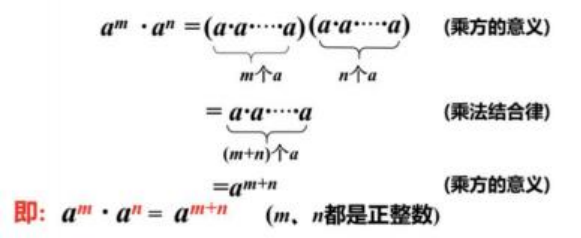
举例子：

$7^8$ x $7^3$ = $7^{8+3}$ = $7^11$

$2^3$ x $2^5$ = $2^{3+5}$ = $2^8$

$3^2$ x $3^2$ = $3^{2+2}$ = $3^4$

2、同底数幂的除法法则：同底数幂相除，底数不变，指数相减 $a^m$ ÷ $a^n$ = $a^{m-n}$

举例子：

$7^8$ x $7^3$ = $7^{8-3}$ = $7^5$

$2^6$ x $2^2$ = $2^{6-2}$ = $2^4$

$3^3$ x $3^2$ = $3^{3-2}$ = $3^1$

3、幂的乘方：底数不变，指数相乘

$(a^m)^ n$ = $a^{mn}$

证明过程：

$(a^m)^ n$ = $a^m$ x $a^m$ x $a^m$ x … $a^m$

​ = $a^{m+m+m+\cdots+m}$ ​ = $a^{mn}$

举例子：

$(10^3 ) ^2$ = $10^6$

$(2^5 )^3$ = $2^{15}$

$(3^3 )^4 = 3^{12}$

4、积的乘方：积的乘方等于把积的每一个因式分别乘方，再把所得结果相乘。

$(ab)^n$ = $a^n$ x $b^n$

举例子：

$(3\times7)^5$ = $3^5$ x $7^5$

$(4\times6)^3$ = $4^3$ x $6^3$