集合
在生活与学习中,为了方便,我们经常要对事物进行分类。
例如,图书馆中的书是按照所属学科等分类摆放的,作文学习可按照文体如记叙文、议 论文等进行,整数可以分成正整数、负整数和零这三类…
在数学中,我们经常用“集合”来对所研究的对象进行分类。把些能够确定的、不同的对象汇集在一起,就说由这些对象组成一个集合(简称:集),组成集合的每个对象都是这个集合的元素。
集合通常用英文大写字母 A, B, C, …表示,
集合的元素通常用英文小写字母 a, b, c, …表示。
元素与集合的关系
如果 a 是集合 A 的元素,记作:a ∈ A 读作: a 属于 A
如果 a 不是集合 A 的元素,记作:a ∉ A 读作: a 不属于 A
比如:如果 A 是由所有小于 10 的自然数组成的集合,则 0 ∈ A, 0.5 ∉ A 。
集合的三大特性
1、确定性: 集合元素必须是确定的。不能确定的对象不能组成集合。
2、互异性:给定一个集合,集合中的元素一定是不同的。若相同的对象归入同一个集合时
只能算作集合中的一个元素。
3、无序性:集合中的元素可以任意排列,与次序无关。
表示方式
1、列举法: 把集合的元素一一列举出来,写在大括号内,元素之间用逗号隔开。 {a, b, c, ……}元素在大括号内,相邻元素之间用逗号隔开。
例如 用两个元素 0 和 1 组成的集合 {0,1}
24 的所有质因数组成的集合 {1,2,3,4,6,8,12,24}
2、描述法:大括号内画一条竖线,竖线的左侧为集合的代表元素,竖线的右侧为元素所具有的特征性质。
例如 平面直角坐标系下,第一象限内所有点组成的集合 A。
A={(x,y) | x>0, y>0}
集合的基本运算
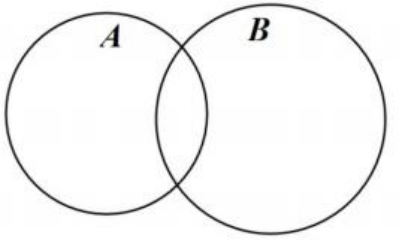
并集
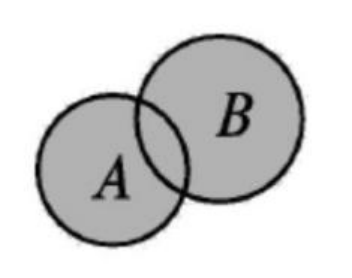
由所有属于集合 A 或属于集合 B 的元素组成的集合,称为集合 A 与 B 的并集。记做 A ∪ B (读做 A 并 B)
A ∪ B = { x | x ∈ A, 或 x ∈ B }
交集
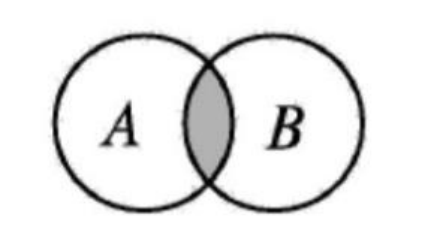
由所有属于集合 A 且属于集合 B 的元素组成的集合,称为集合 A 与 B 的交集。记做 A ∩ B (读做 A 交 B)
A ∩ B = { x | x ∈ A, 且 x ∈ B }
补集
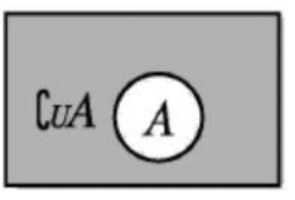
设 U 是全集,A 是 U 的一个子集(即 A⊆U),则 U 中所有不属于 A 的元素组成的集合,叫做 U中子集 A 的补集。记作:
= { x | x ∈ U, 且 x ∉ A }
容斥原理
设有两个非空集合 A,B,记 |S| 为集合 S 中元素的个数,则有如下关系
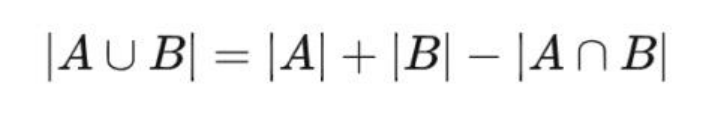
练习
1、 设 A={1,2,3,4,6}, B={2,4,5,6}。求 A ∪ B
2、设 A={1,2,3,4,6}, B={2,4,5,6}。求 A ∩ B