什么是搜索算法？

搜索就是在一定范围内，逐个寻找合适答案。所以搜索本质上也是枚举。传统的循环枚举事先是知道循环的次数和范围。而搜索的枚举过程比循环更加灵活，搜索时从一个状态出发，通过状态的可行性判断，从而扩大搜索的范围，直到找到解或者找到无解状态为止。

什么是DFS？

深度优先搜索算法（Depth First Search，DFS) ，简称深搜，或回溯法、试探法。是一种常用的图遍历算法，用于在图或树数据结构中遍历所有节点。从一个起始节点开始，沿着一条路径尽可能远地访问节点，直到到达不能继续前进的节点，然后返回上一层继续探索其他路径。这个过程是递归的，通过不断地深入进入节点的子节点，直到遍历完整个图, “递”的过程就是往下搜的过程对应着深度，“归”的过程就是回溯，回退上一级。

从一条路走到底，能进则进，不能进则退。

为了求得问题的解，先选择某一种可能情况向前探索，在探索过程中，一旦发现原来的选择是错误的，就退回上一步重新选择条件，继续向前探索，如此反复进行，直至得到解或证明无解。

深搜使用场景

方案枚举问题

排列问题：N个数按一定规则全排列，有几种排列方式
组合问题：N个数里面按一定规则找出k个数的集合

[info] 什么是组合，什么是排列？

组合是不强调元素顺序的，排列是强调元素顺序。

例如：{1, 2, 3} 和 {2, 1, 3} 在组合上，就是一个集合，因为不强调顺序，而要是排列的话，{1, 2, 3} 和 {2, 1, 3} 就是两个集合了。

可重复的搜索模板

void dfs(int x){//x代表的是搜索的第x步 
    if(到达目的地){
        输出解;
        return; 
    }
    for(int i=1;i<=方案数;i++){//枚举当前第x步走的所有可能方案 
        if(方案可行){
            保存方案 
            dfs(x+1);//搜索下一步 
        }
    }
}

不可重复搜索模板

void dfs(int x){//x代表的是搜索的第x步 
    if(到达终点){
        输出解||保存解;
        return; 
    }
    for(int i=1;i<=方案数;i++){//枚举当前第x步走的所有可能方案 
        if(方案可行){
            保存方案i
            标记方案i已用 
            dfs(x+1);
            恢复保存结果之前的状态(解除方案i)
        }
    }
}

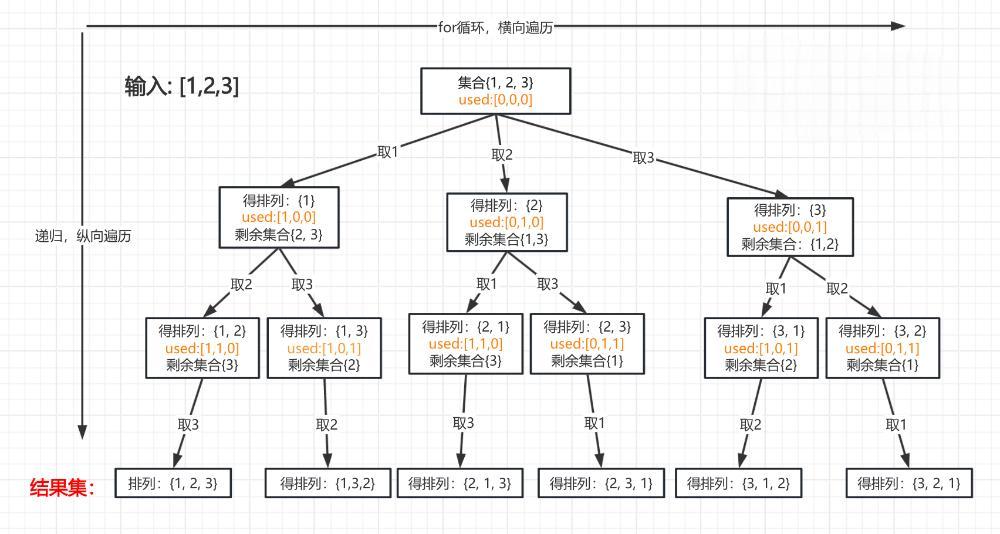
例题分析—全排列

输出自然数 1到 n 所有不重复的排列，即 n的全排列，要求所产生的任一数字序列中不允许出现重复的数字。

解题思路

(1)定义两个数组，一个用来存放题目答案的，一个用来标记某个数在某一轮中是否被使用过。

(2)写一个输出函数，一旦填满了数就直接输出。

(3)在循环中先判断填的数是否用过，如果没有就填入，搜索下一格。

#include<bits/stdc++.h>
using namespace std;
int n,ans[10];//ans是结果数组
bool v[10];//v数组是判断是否用过这个数
void print() { //输出函数
   for(int i=1; i<=n; i++)
       cout<<setw(5)<<ans[i];//保留5位场宽
   cout<<endl;
}
void dfs(int x) { //深搜函数，当前是第k格
   if(x>n) { //填满了的时候
       print();//输出当前解
       return;
   }
   for(int i=1; i<=n; i++) { //1-n循环填数
       if(v[i]==0) { //如果当前数没有用过
           v[i]=1;//标记一下,1表示当前这个数字使用过
           ans[x]=i;//把这个数填入结果数组
           dfs(x+1);//填下一个
           v[i]=0;//回溯
       }
   }
}
int main() {
   cin>>n;
   dfs(1);//注意，这里是从第1格开始的！
   return 0;
}

路径搜索问题

路径搜索也就是迷宫问题，一般来说时在矩阵地图中进行搜索，目标是找出满足要求的路径数量、路径长度、或者是求出满足要求的路径权值和等。明显，在迷宫问题中，每一步都是需要试探的，走不通情况下要原路返回。

方向偏移

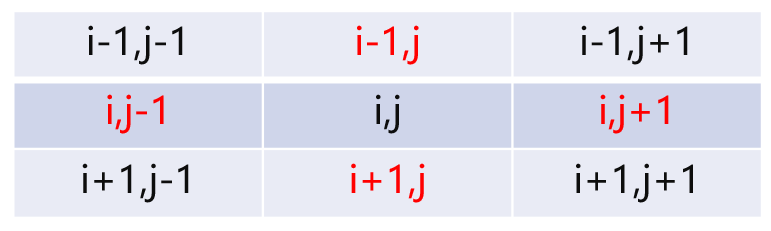
迷宫常用模板

//设置dx、dy方向数组
int dx[4]={-1,1,0,0};//上下左右 4个方向 
int dy[4]={0,0,-1,1};//上下左右 4个方向 
void dfs(int x,int y){
    if(找到目标){
        return;
    }
    for(枚举下一步可以到达的坐标,xx和yy){
        if(可以向下走){
            标记(xx,yy);
            dfs(xx,yy);
            取消标记(xx,yy);
        }
    }
}

泛洪法求连通区域

泛洪法，理解起来也很形象，就是像洪水一样，水将连通的地方全部淹没。这样，只要所有连通的地方都找出来，就很容易统计出连通区域的数量，泛洪法也称染色法，一般用来求解连通区域问题。

算法模板

void dfs(int x,int y){//一般来说区域坐标为二维坐标 
    把(x,y)染色;
    for(int i=0;i<=临街位置数;i++){
        if(邻接位置可达){//包括访问和位置性质 
            dfs(邻接位置)
        }
    } 
}

09-深度优先搜索