什么是排序算法?
排序是日常生活中十分常见的现象,例如按照成绩高低进行排序、按照身高从矮到高排队等。
排序算法是一种用于将一组元素按照一定规则排列的算法。这种排序可以按照升序(从小到大)或降序(从大到小)的方式进行。排序算法是计算机科学中的基本问题之一,因为在实际应用中,经常需要对数据进行排序以便更方便地进行搜索、查找或其他操作。
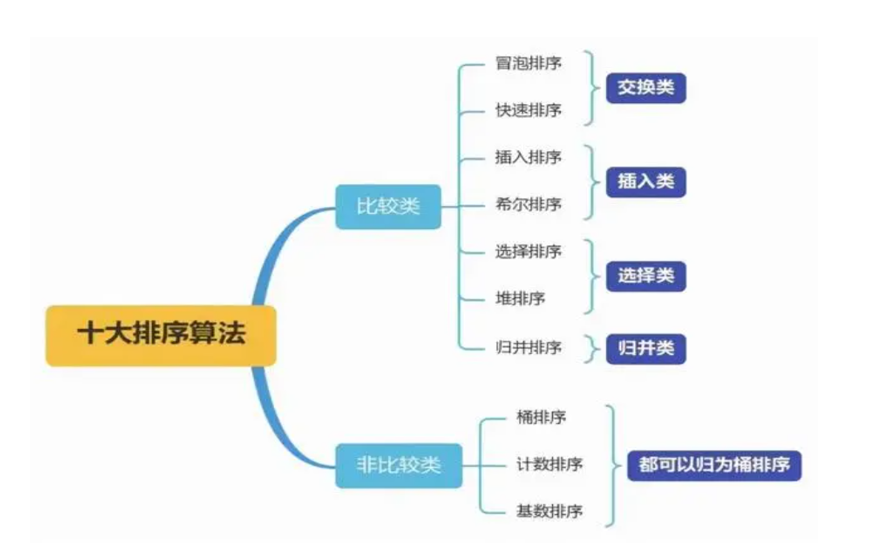
相关概念
稳定性:相等的元素经过排序之后相对顺序是否发生了改变
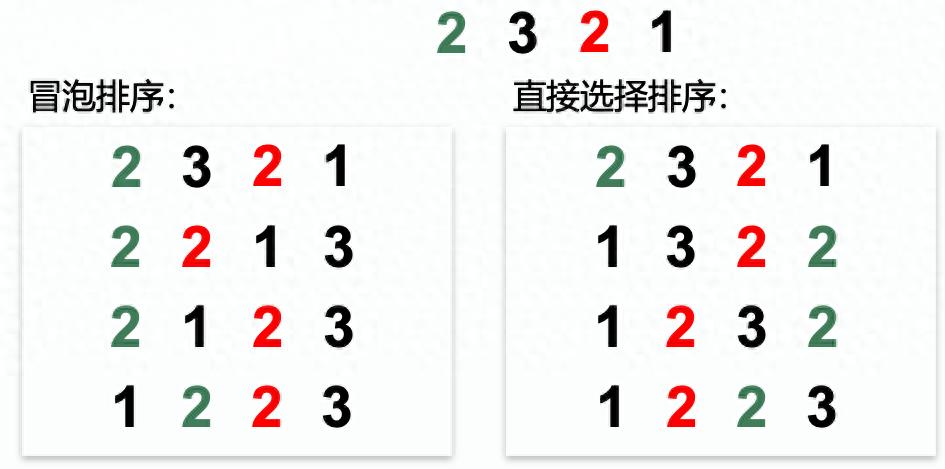
- 稳定:如果排序前a在b的前面,且a==b,排序之后a仍然在b前面,称该算法稳定
- 不稳定:如果排序前a在b前面,且a==b,排序之后a可能在b后面,称该算法不稳定
- 时间复杂度:排序数据时总的操作次数。反映当n变化时,操作次数呈现的变化规律。
- 空间复杂度:指算法在计算机内执行时所需存储空间的度量。
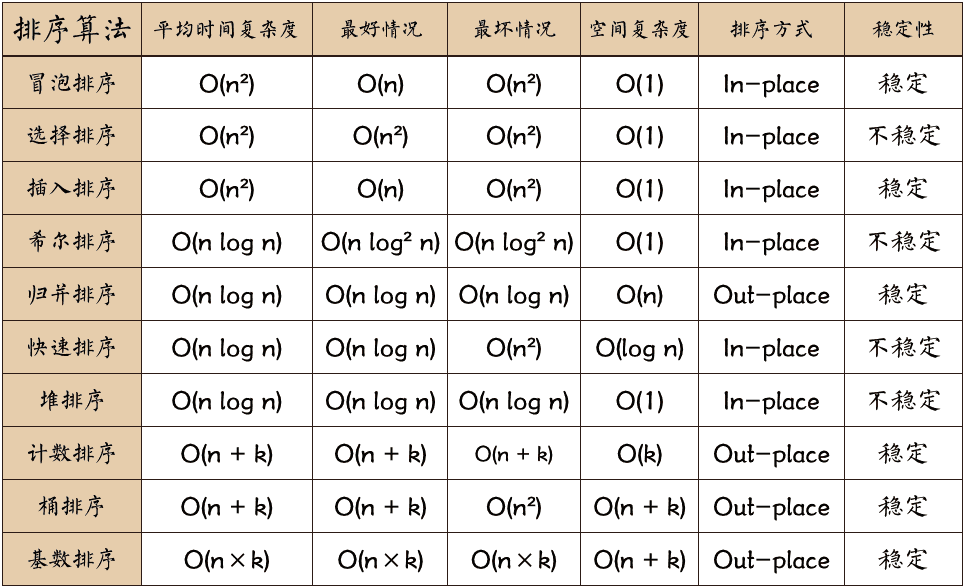
基于比较的三大基础排序
冒泡排序
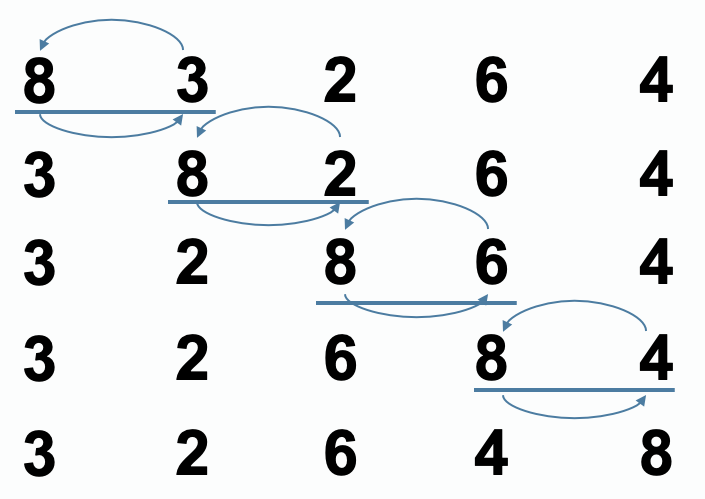
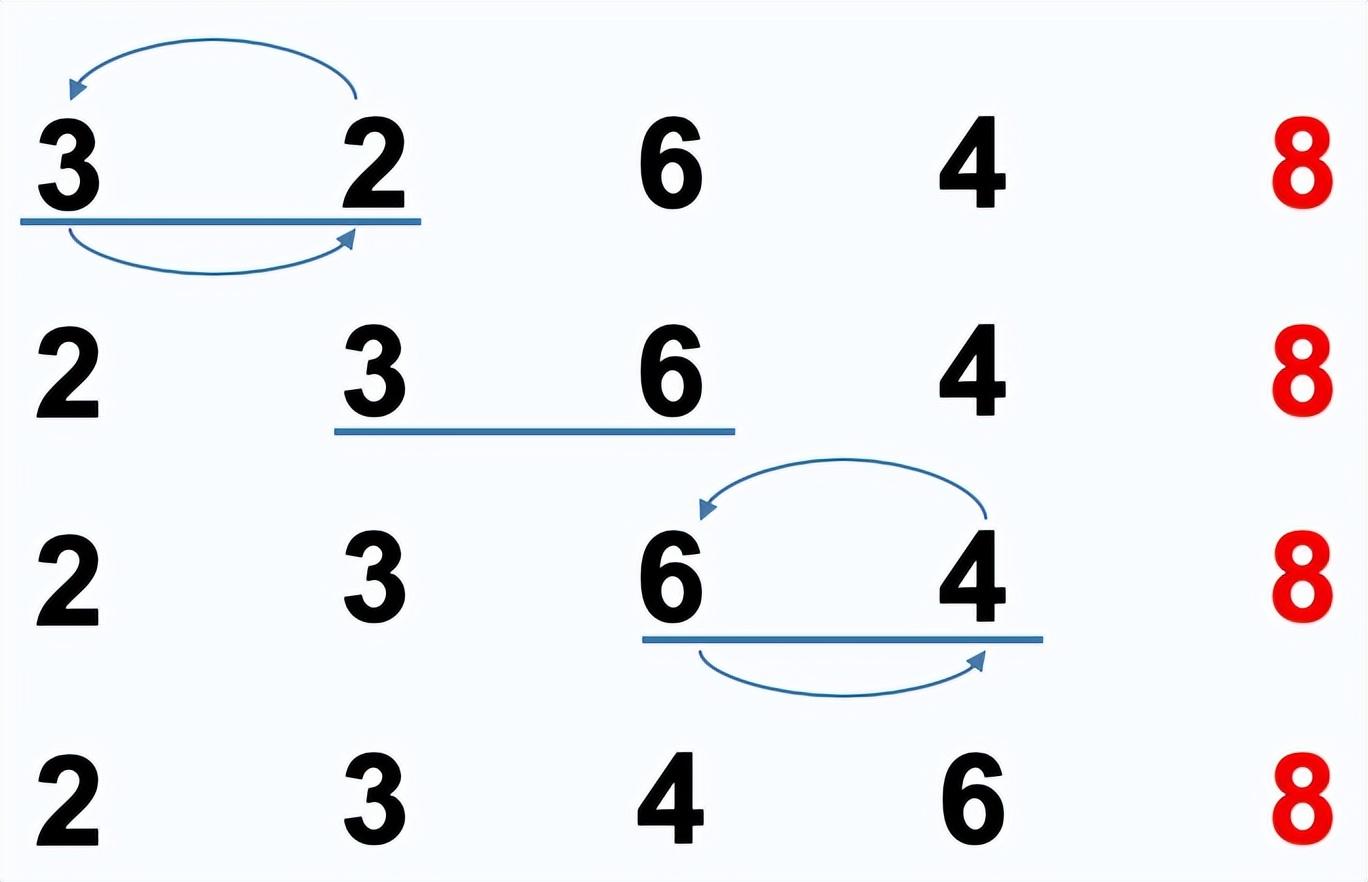
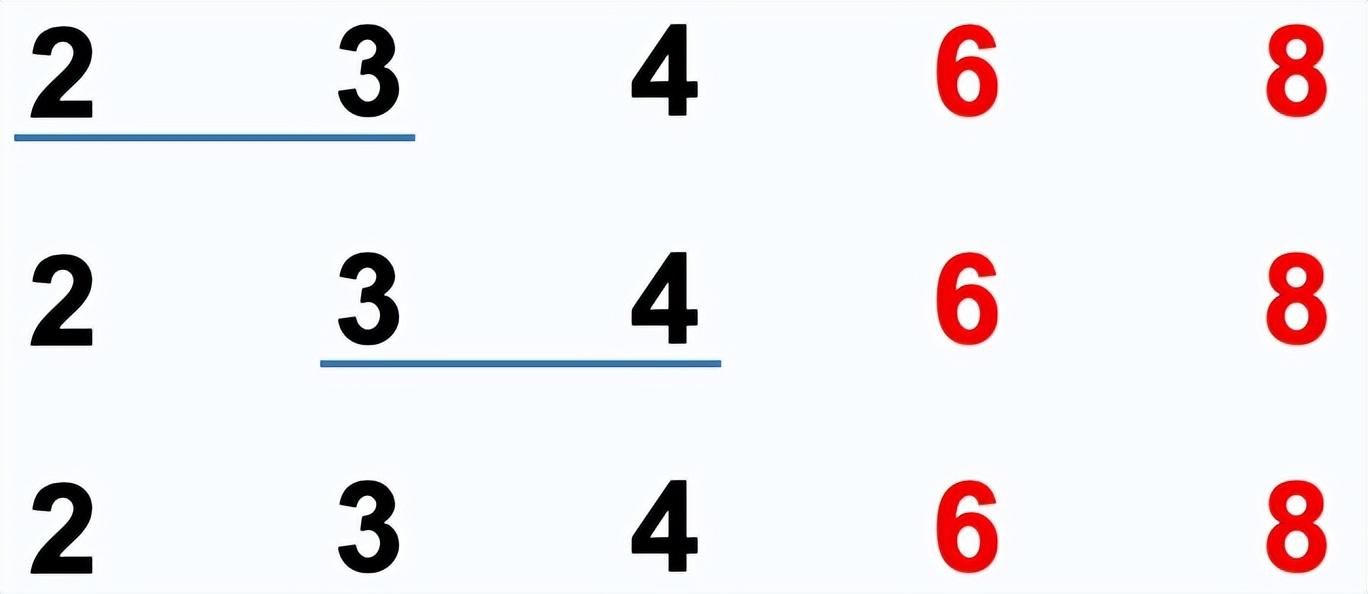
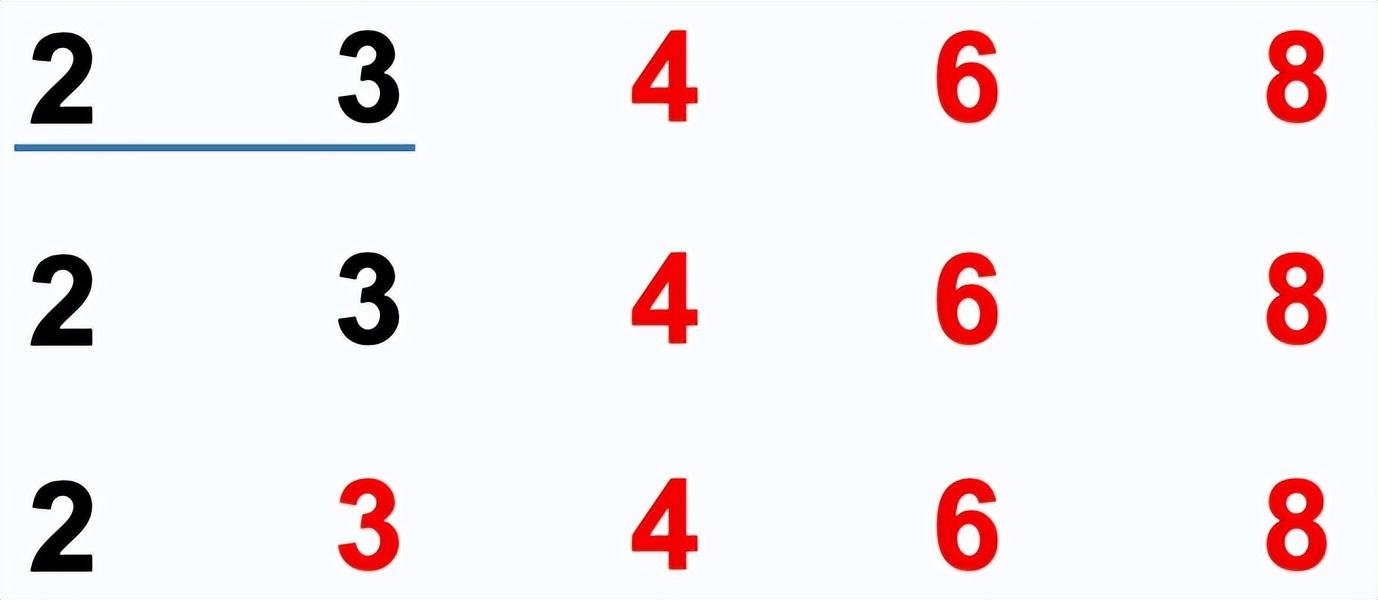
冒泡排序:依次比较两个相邻的元素,如果顺序错误就把他们交换过来。每次冒泡,最大(最小)的元素会经由交换“浮”到序列顶端。多次冒泡后,即可完成排序。
排序过程:
- 比较相邻的元素。如果第一个比第二个大,就交换它们两个
- 对每一对相邻元素做同样的工作,从开始第一个对到结尾的最后一对,这样的最后的元素就是最大的数。
- 针对所有的元素重复以上的步骤,除了最后一个。(一趟下来,最大的那个数就排在了最后面,那么下一趟对前n-1个数做同样的操作,重复步骤1-3,直到排序完成)
时间复杂度:O(n2),稳定。
冒泡排序——基础版
#include <iostream>
using namespace std;
int a[101],n;
int main(){
cin >> n;
for(int i = 1; i <= n; i++) {
cin >> a[i];
}
for(int i = 1; i <= n-1; i++){
for(int j = 1; j <= n - i; j++){
if(a[j] > a[j + 1])
swap(a[j], a[j + 1]);
}
}
for(int i = 1; i <= n; i++) {
cout << a[i] << " ";
}
return 0;
}
冒泡排序优化——提前跳出:如果序列已经有序,就没有必要进行后面的循环。
#include <iostream>
using namespace std;
int a[101],n;
int main(){
cin >> n;
for(int i = 1; i <= n; i++) {
cin >> a[i];
}
for(int i = 1; i <= n-1; i++){
bool flag=true;
for(int j = 1; j <= n - i; j++){
if(a[j] > a[j + 1]){
flag=false;
swap(a[j], a[j + 1]);
}
}
if(flag) break;
}
for(int i = 1; i <= n; i++) {
cout << a[i] << " ";
}
return 0;
}
选择排序
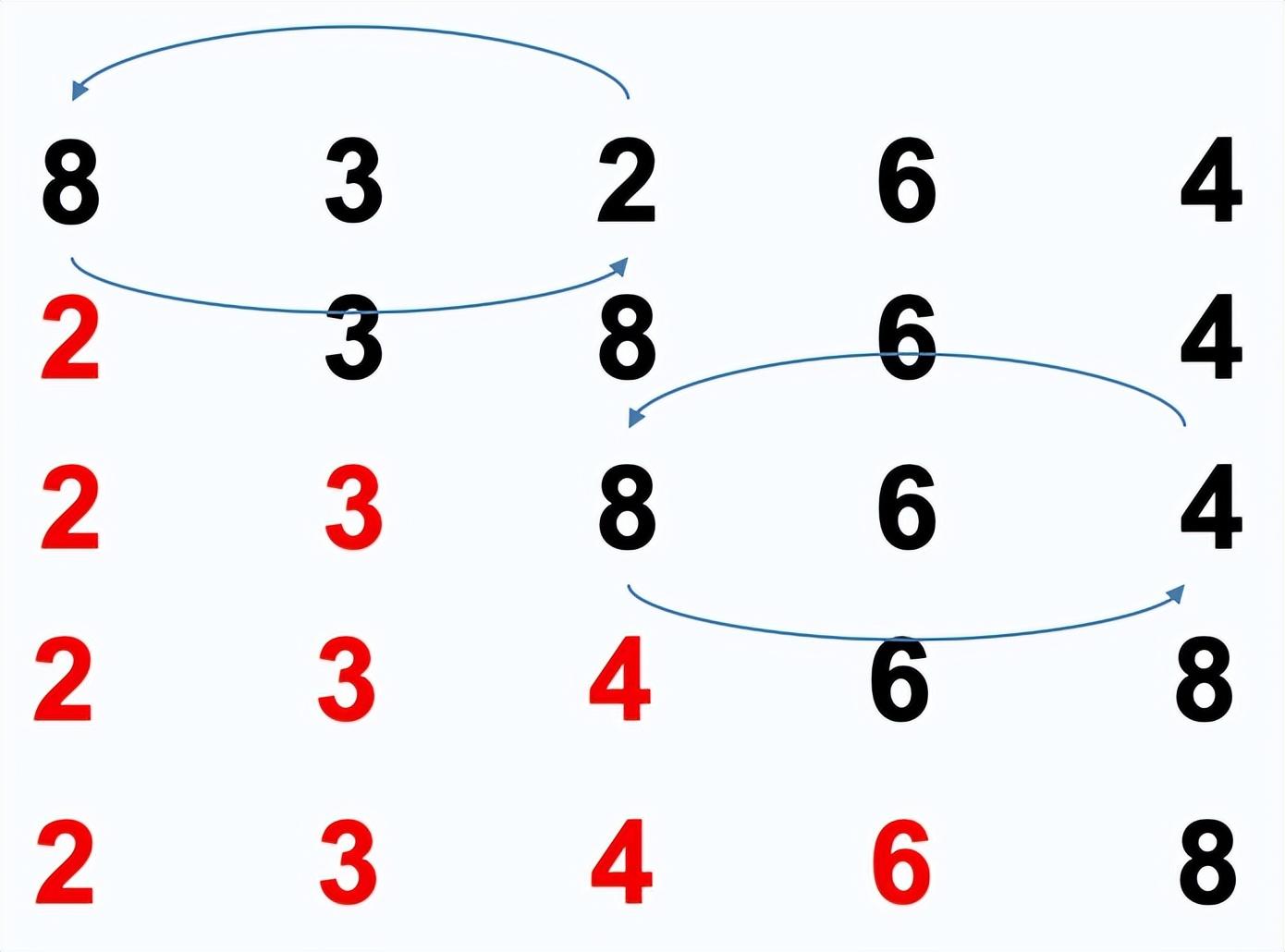
选择排序:每一趟从待排序的数据元素中选出最小(或最大)的一个元素,顺序放在待排序的数列的最前面。
排序过程:
- 在未排序的数列中找到最小元素,存放到已排序数列的结束位置的下一个位置。
- 从剩余未排序元素中继续寻找最小元素,然后放到已排序序列的末尾。
- 重复1-2步骤
时间复杂度:O(n2), 不稳定。
#include <iostream>
using namespace std;
int a[1001],n;
int main() {
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n-1;i++){
int mini=i;//打擂台,记录擂主
for(int j=i+1;j<=n;j++) {
if(a[j]<a[mini]) {
mini=j;
}
}
if(i!=mini)
swap(a[i],a[mini]);
}
for(int i=1;i<=n;i++) {
cout<<a[i]<< " ";
}
return 0;
}
插入排序
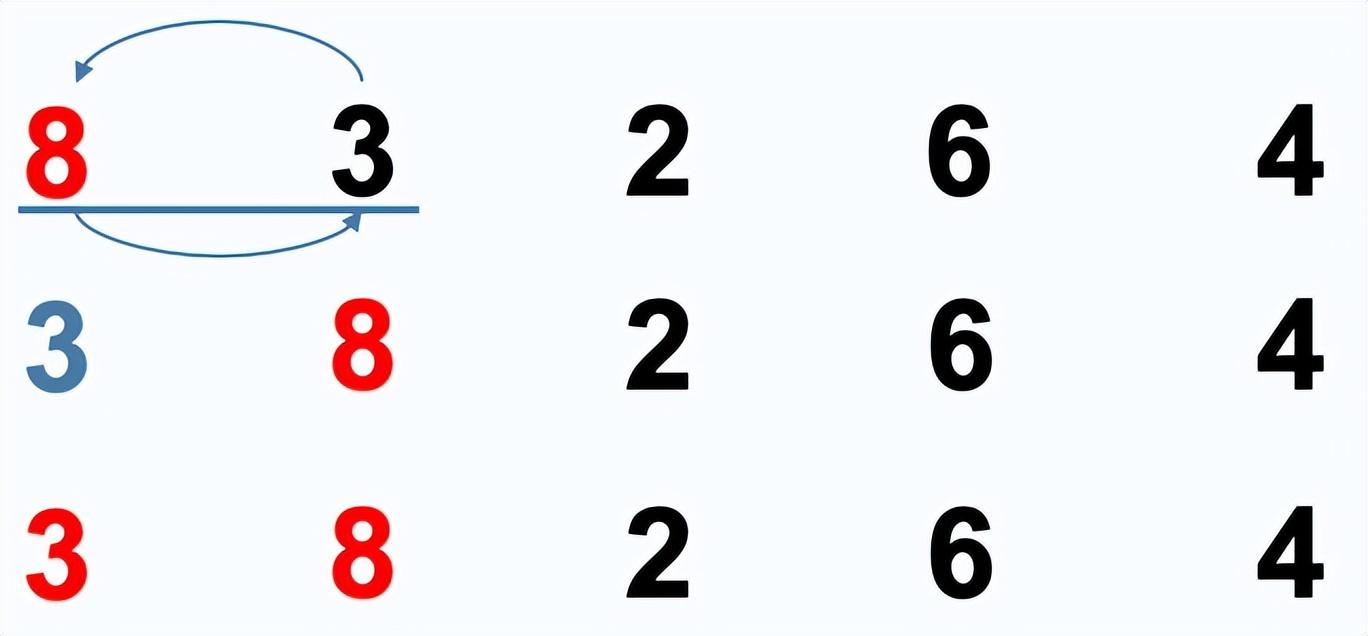
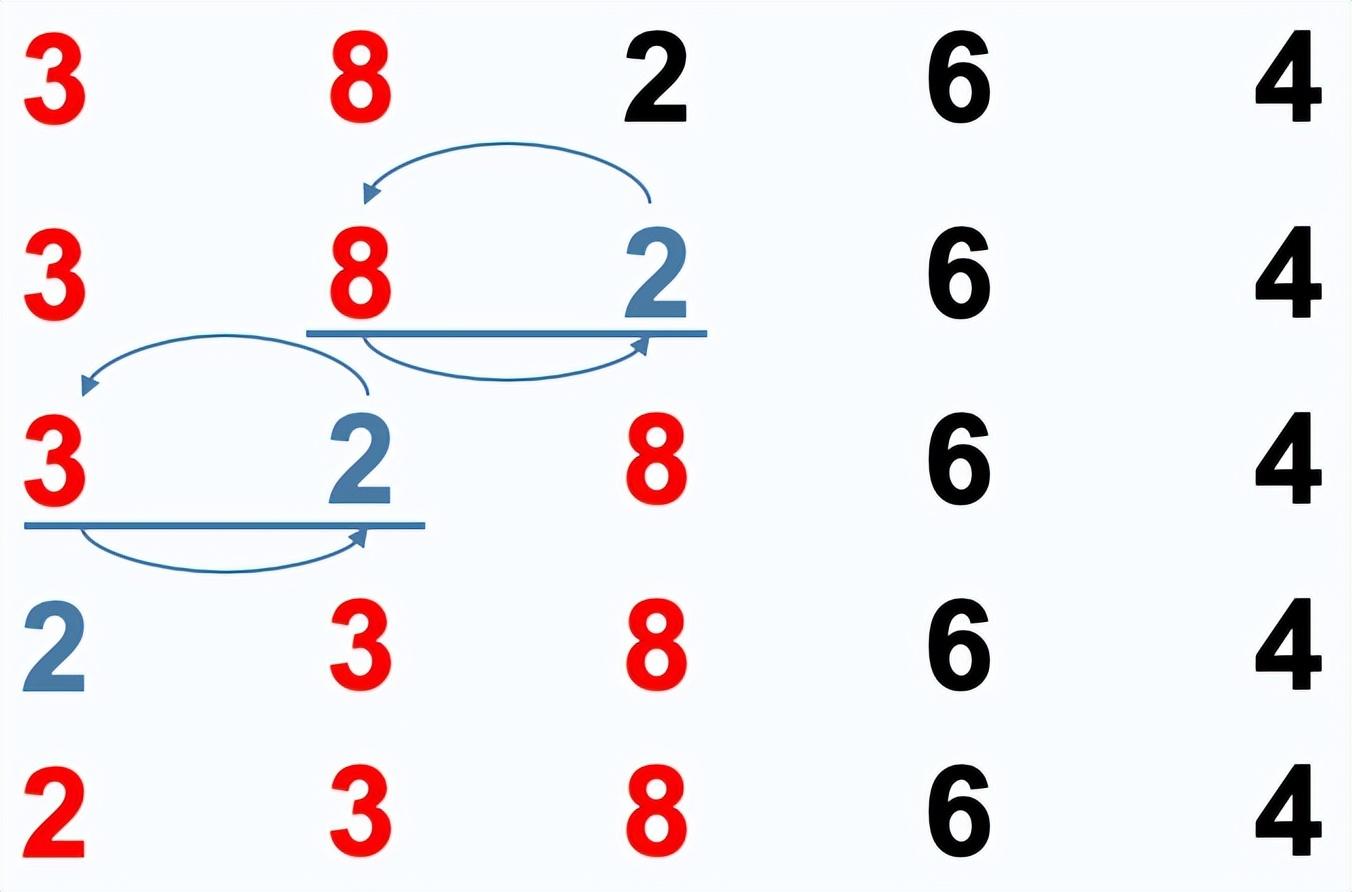
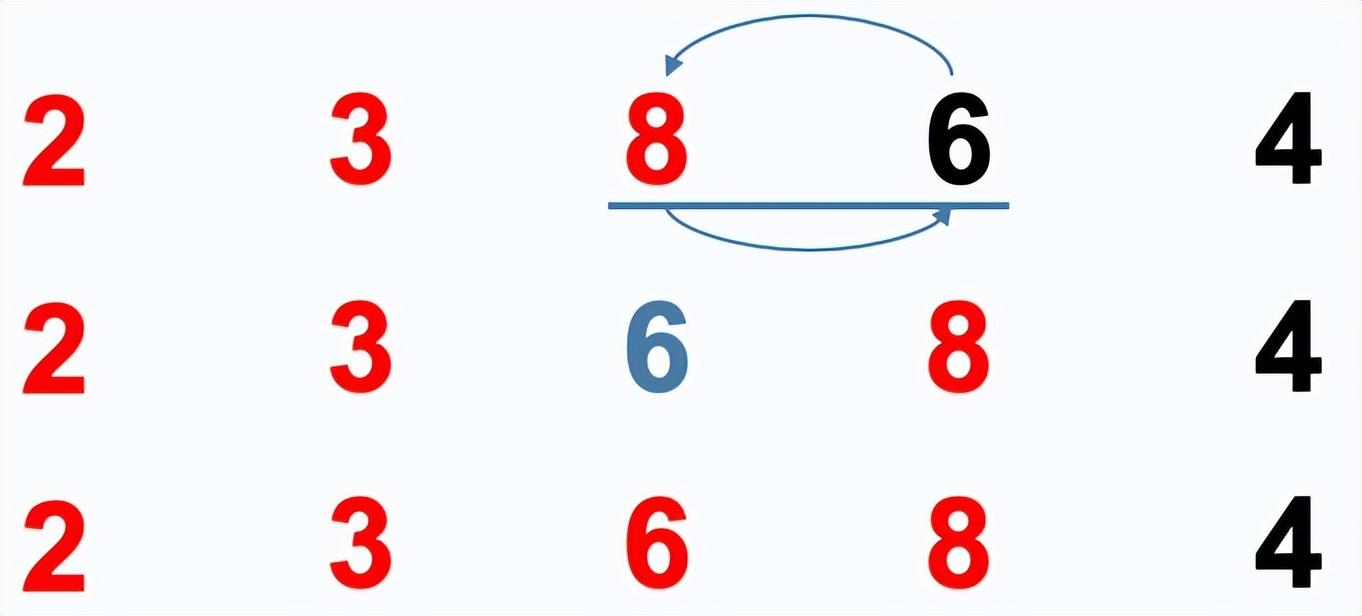
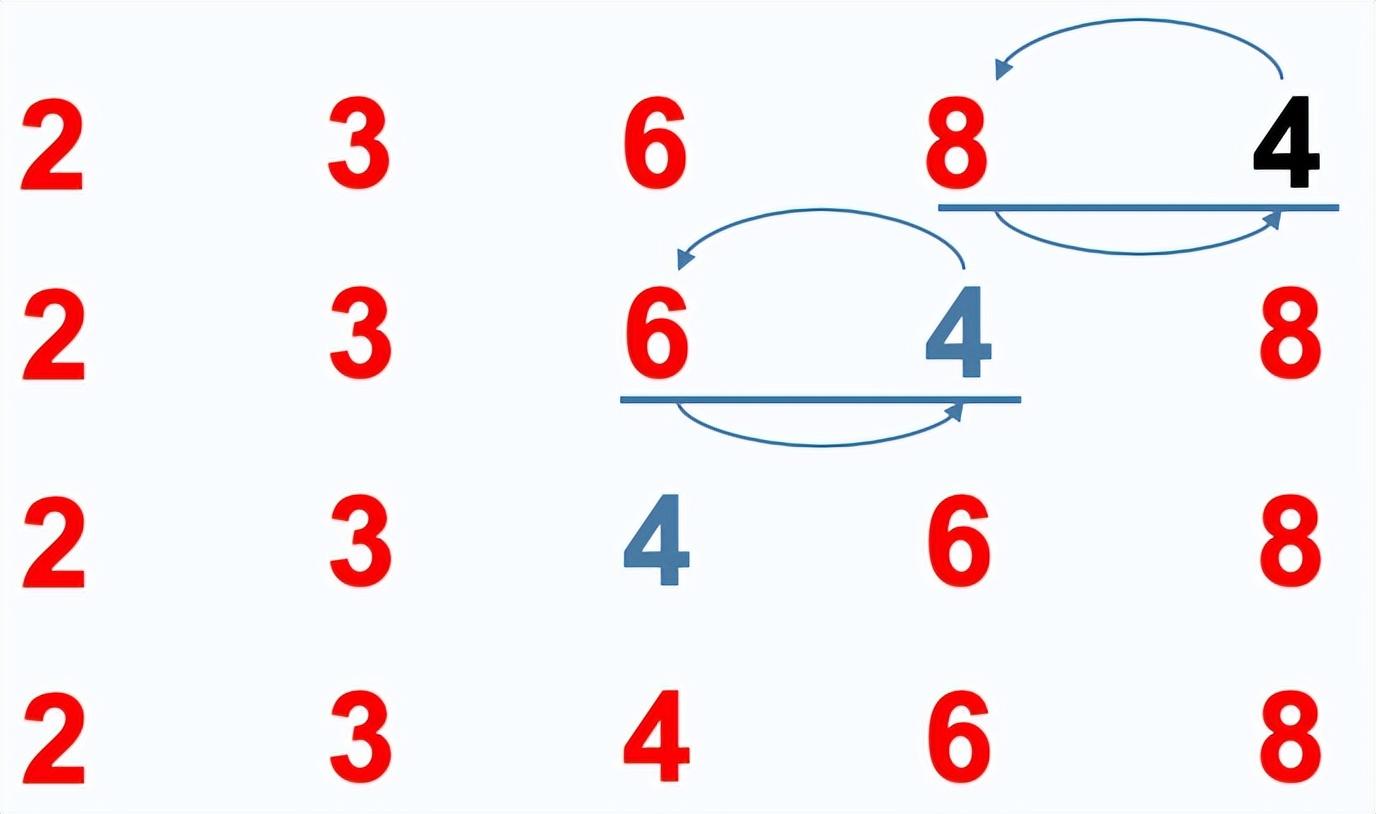
插入排序:通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
排序过程:
- 从第一个元素开始,该元素认为已经被排序
- 取出下一个元素值,在已经排序的元素序列中从后向前扫描
- 如果在已排序序列扫描到的元素值大于新元素值,将扫描到的元素移到下一位置
- 重复步骤3,直到找到已排序的元素小于新元素的位置
- 将新元素插入到该位置后一个位置,完成一个元素的排序
- 从接下来的n-1个开始,重复步骤2-5,直到完成全部数据排序。
时间复杂度:O(n2), 稳定。
方法1:
#include <bits/stdc++.h>
using namespace std;
int n,a[1001];
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=2;i<=n;i++){
int j=i-1,x=a[i];
while(j>=1&&x<a[j]){
a[j+1]=a[j];//有序的元素向后移动
j--;//继续往前看
}
a[j+1]=x;
}
for(int i=1;i<=n;i++){
cout<<a[i]<<" ";
}
return 0;
}
方法2:
#include <bits/stdc++.h>
using namespace std;
int n,a[1001];
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=2;i<=n;i++){
int j=i;
while(j>=1&&a[j]<a[j-1]){
swap(a[j],a[j-1]);//直接交换元素
j--;//继续往前看
}
}
for(int i=1;i<=n;i++){
cout<<a[i]<<" ";
}
return 0;
}
基于分类的三大排序
计数排序
计数排序:是一种特殊的桶排序。桶的个数是可能出现的数据种类数。
计数数组:数组下标是桶的编号,通常为数据值,数组的值表示数据个数。
适用条件:待排序数据为整数,数据范围有限。
设数据个数为n,数据范围为k。
时间复杂度:O(n+k),额外空间复杂度:O(k),稳定。
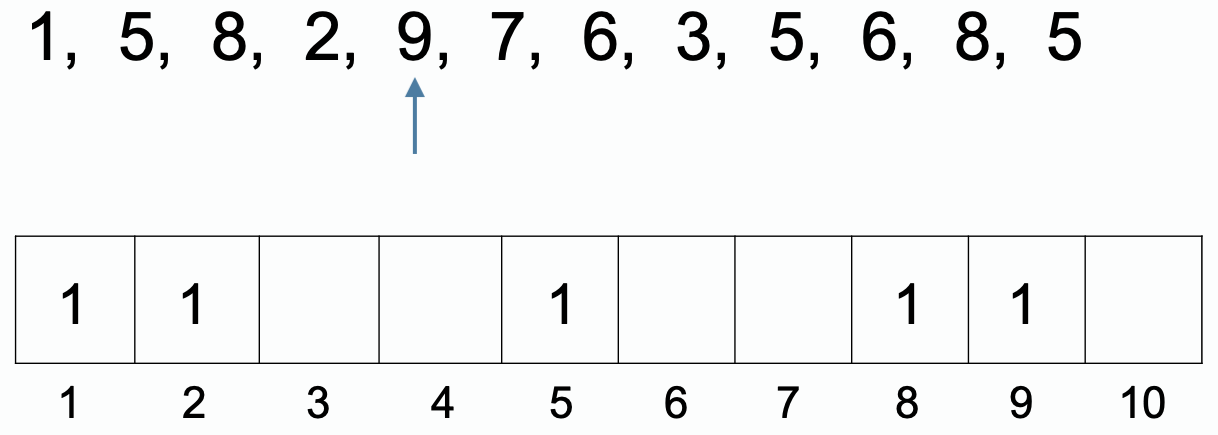
最终数组:

#include <bits/stdc++.h>
using namespace std;
int n,a[1001],num;
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>num;
a[num]++;
}
for(int i=0;i<=1000;i++){
for(int j=1;j<=a[i];j++){
cout<<i<<" ";
}
}
return 0;
}
桶排序
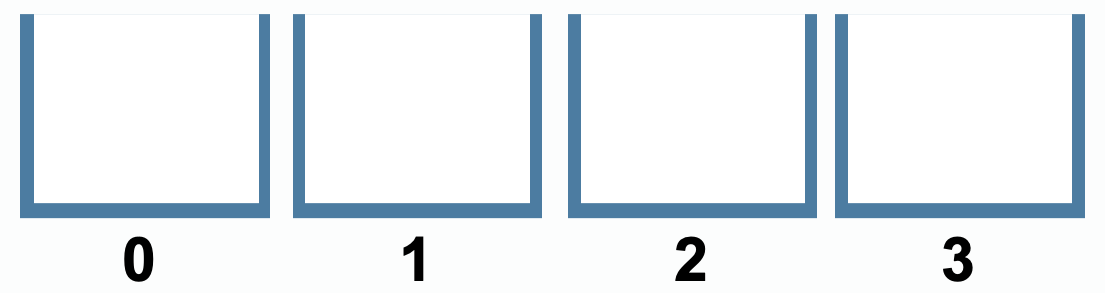
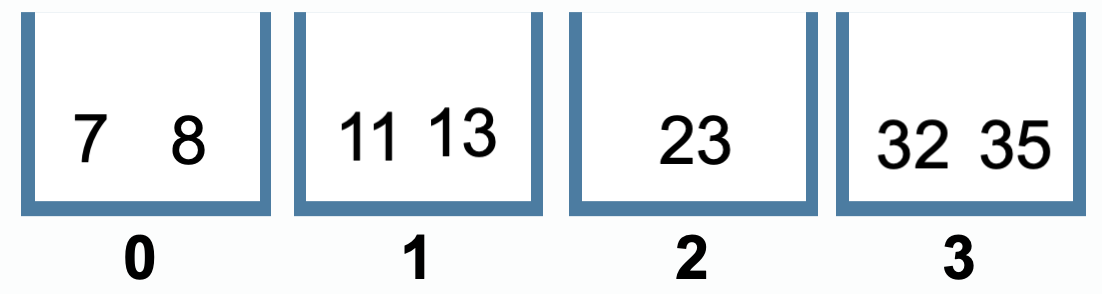
桶排序:将数据分到有限数量的有序的桶里,每个桶内分别排序,最后将各个桶中的数据合并。
数据分配到桶:散列过程

基数排序
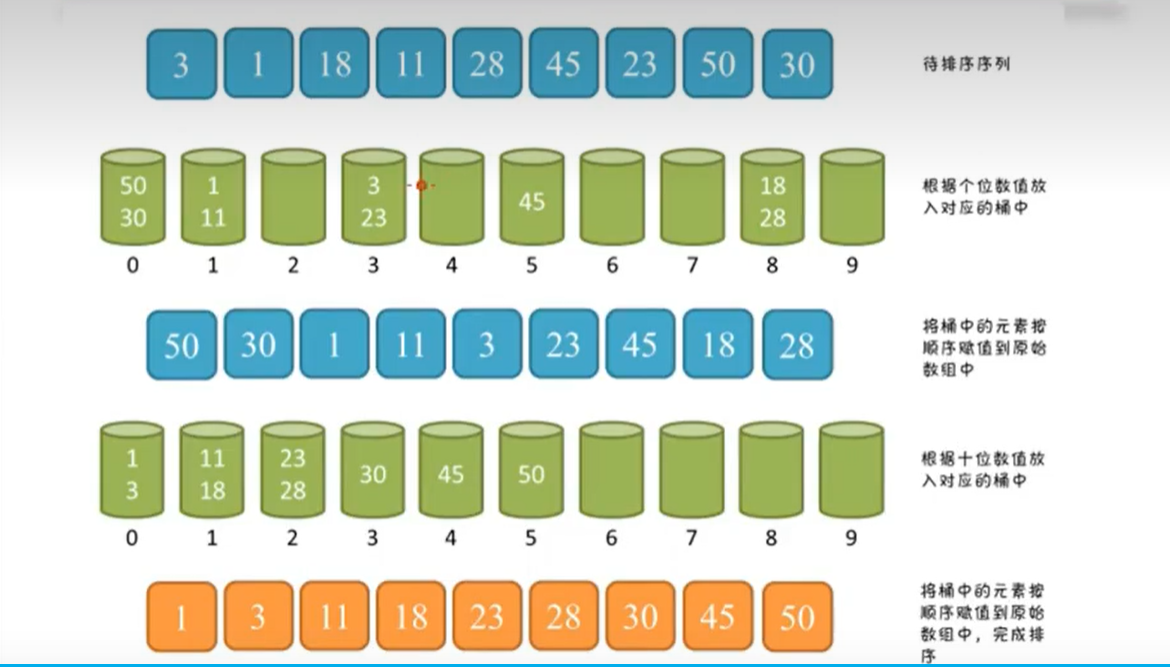
基数排序(Radix Sort)是桶排序的扩展,也是一种非比较型整数排序算法。
原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。
小结
计数排序、桶排序、基数排序都是基于分类的思想,利用了桶的概念,只是分类的依据不一样
计数排序:每个桶只存储单一值
桶排序:每个桶存储一定范围的数值
基数排序:根据值的每位数字来分配
sort排序函数
为什么使用sort?
排序非常常见,每次都自己写很麻烦存在选择的困扰:究竟用哪个排序好呢?
sort:近似优化后的快排,同时结合了其它排序
sort(begin,end,[cmp])
//begin:开始的地址 end:结束的地址
//cmp:比较的方式,如果不写的话默认调用<
比较函数:传入两个数组中元素类型的参数,返回第一个参数排在前面的条件。
若不写比较函数cmp,默认为升序排序。

#include <bits/stdc++.h>
using namespace std;
int n,a[1001];
bool cmp(int &a,int &b){
return a>b;
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
sort(a+1,a+1+n,cmp);
for(int i=1;i<=n;i++){
cout<<a[i]<<" ";
}
return 0;
}