前言
在编程竞赛中,数学基础是许多算法和问题求解的核心,尤其是在中国计算机学会(CSP-J)竞赛中,初等数论常常是考察的重点。初等数论研究整数的基本性质及其应用,涵盖了如最大公因数、最小公倍数、质数、同余理论等基本概念和方法。掌握这些内容不仅有助于解答数论相关题目,还能为后续学习复杂的算法打下坚实的基础。
初等数论是什么
初等数论是研究数的规律,特别是整数性质的数学分支。
因数与倍数
定义:整数a除以整数b(b≠0) 除得的商正好是整数而没有余数,我们就说a能被b整除,或b能整除a。a称为b的倍数,b称为a的因数(约数)。
12=3 x 4
12是3的倍数,3是12的因数。3能整除12,或12能被3整除
判断两个数能否被整除
bool candiv(int a, int b){
return a % b == 0;
}
质数与合数
质数(又称素数):是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数。
例如2、3、5、7、11、13、17、19等都是质数
[info] 注意
1 既不属于质数也不属于合数
2是最小的质数,且为唯一的偶质数
质数的个数是无限的
合数:在大于1的整数中除了能被1和本身整除外,还能被其他数(0除外)整除的数。
例如 4、6、8、9、10、12、14、15等都是合数
合数至少有三个正因数,除1和本身以外还有至少一个正因数
质因数
定义:如果一个正整数a有一个因数b,而b又是质数,则b就叫做a的质因数。
例如12=3 x 4,3是质数,而3不是质数,所以3是12的质因数,而4不是12的质因数。
唯一分解定理
定义:任何一个大于1的正整数都能唯一分解为有限个质数的乘积。其中每个质数都是这个合数的因数。
最大公约数与最小公倍数
几个自然数公有的约数,叫做这几个自然数的公约数。公约数中最大的一个公约数,称为这几个自然数的最大公约数。
辗转相除法: 用较大数除以较小数,得到余数。 若余数为0,那么上一次除法中的除数就是最大公约数。 若余数不为0,那么下一次的除法为上一次除法中的除数除以余数。 重复这一过程,直到得到最大公约数 。
两个或多个整数公有的倍数叫做它们的公倍数,其中除0以外最小的一个公倍数就叫做这几个整数的最小公倍数。
若两个整数a,b的最大公约数是gcd(a,b),最小公倍数是lcm(a,b),那么有:
a * b = gcd(a,b) * lcm(a,b)
lcm(a,b) = a / gcd(a,b) * b
同余定理
同余关系
给定一个正整数m,如果两个整数a和b满足(a-b)能够被m整除,即(a-b)/m得到一个整数,那么就称整数a与b对模m同余,记作a≡b(mod m)。
a≡b(mod m),即两个整数a、b除以整数m所得的余数相等。
①反身性:a ≡ a(mod m)
②对称性:若 a ≡ b(mod m),则 b ≡ a(mod m)
③传递性:a ≡ b(mod m),b ≡ c(mod m),则 a ≡ c(mod m)
④同余式相加: a ≡ b(mod m),c ≡ d(mod m),则 a ± c ≡ b ± d(mod m)
⑤同余式相乘:a ≡ b(mod m),c ≡ d(mod m),则 ac ≡ bd(mod m)
⑥线性运算:a ≡ b(mod m),c ≡ d(mod m),则 a ± c ≡ b ± d(mod m),a c ≡ b d(mod m)...
同余定理加法乘法应用
(a + b)%m = (a%m + b%m)%m
(a - b)%m = (a%m - b%m)%m
(a b)%m = (a%m b%m) %m
如果只有加、减、乘运算,求结果对m取模,可以在运算的过程中让中间结果对m取模。
例:(a+b*c)%m = (a%m + (b%m * c%m)%m)%m
平面直角坐标系
在平面内画两条互相垂直,并且有公共原点的数轴。 其中横轴为X轴,纵轴为Y轴。 这样我们就说在平面上建立了平面直角坐标系。
坐标系中表示点的坐标 (x坐标, y坐标)
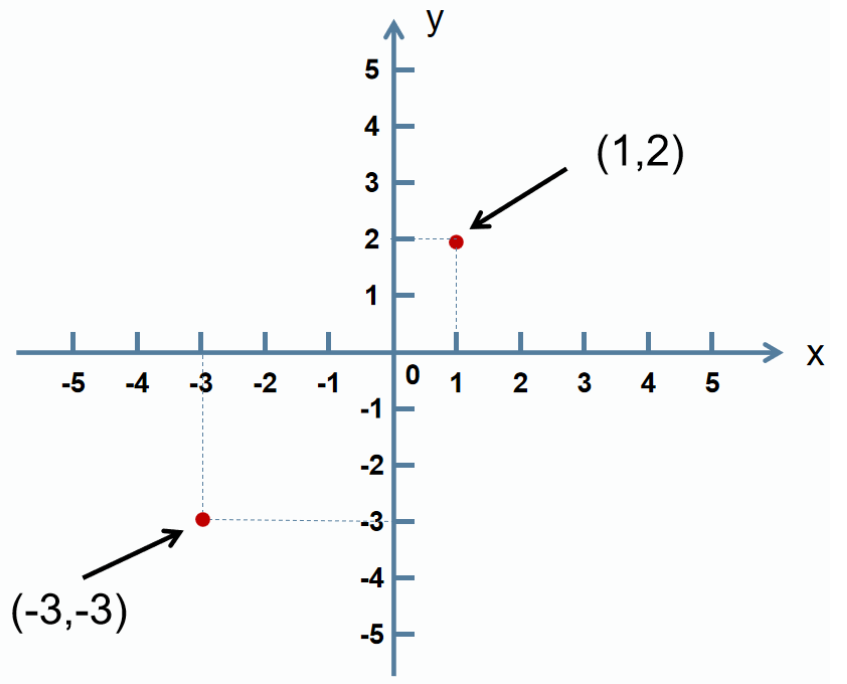
两点距离公式
已知两点 两点间距离公式:dis =
<cmath>数学库中的函数
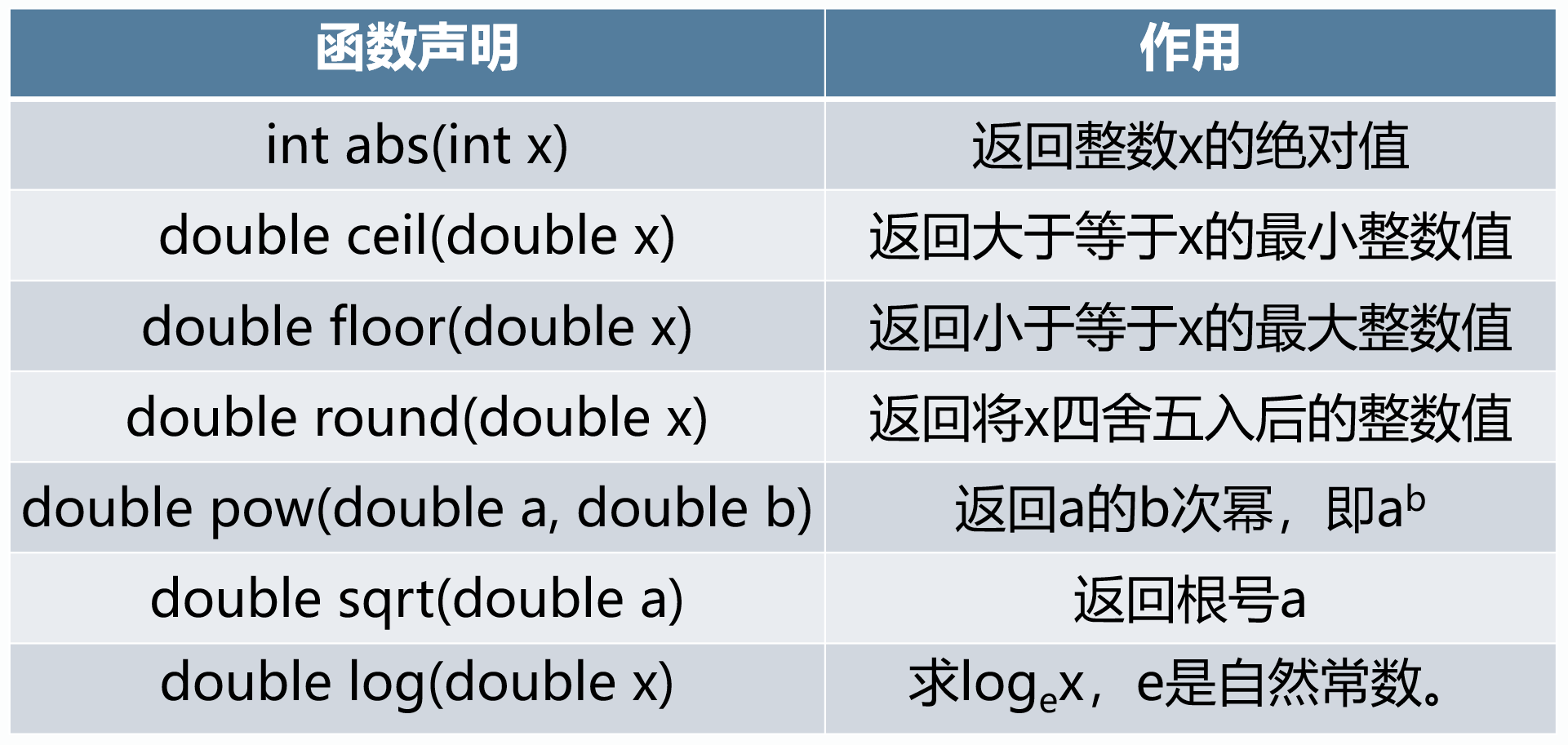
cout<<ceil(3.5)<<" "<<ceil(-3.5)<<endl; //向上取整
cout<<floor(3.5)<<" "<<floor(-3.5)<<endl;// 向下取整
cout<<int(3.5)<< " "<<int(-3.5)<<endl;// int 取整
cout<<sqrt(2)<< " " <<sqrt(9)<<endl;// 开平方
cout<<pow(2,10)<<endl;// 乘方\幂
cout<<round(3.5)<<" "<<round(3.49)<<endl;// 四舍五入
cout<<int(3.5 + 0.5)<<endl;
输出
4 -3
3 -4
3 -3
1.41421 3
1024
4 3
4