最大公约数

最大公约数（greatest common divisor，简写为 gcd）。

设 $a1$ 和 $a2$是两个整数，如果 $a1$ 能被 $d$ 整除，$a2$ 也能被 $d$ 整除，那么 $d$ 就被称为 $a1$ 和$a2$的公约数。其中最大的称为 $a1$ 和 $a2$ 的最大公约数。

分解质因数

每个合数都可以写成几个质数相乘的形式，其中每个质数都是这个合数的因数（约数），叫 做这个合数的质因数。

质因数既是质数，也是因数。

把一个合数用质因数相乘的形式表示出来，叫做分解质因数。

如何求最大公约数？

求 $9$ 和 $18$ 的最大公约数？

$9 = 3 \times 3$

$18 = 2 \times 3 \times 3$

求几个数的最大公约数，先把这些数分解质因数，再将质因数的公共部分相乘即可。

分解质因数

短除法：

把一个合数分解质因数，先用一个能整除这个合数的质数（通常从最小的2开始）去除： 得出的商如果是质数，就把除数和商写成相乘的形式； 得出的商如果是合数，就按照上面的方法继续除下去，直到得出的商是质数为止； 最后把各个除数和最后的商写成相乘的形式。

把一个合数用质因数相乘的形式表示出来叫做分解质因数

注意

分解质因数只适合求比较小的整数的最大公约数。

对于比较大的整数，用分解质因数求它们的最大公约数就会比较麻烦，因为整数越大，写成 分解质因数的方式就越困难。

例如：求 8251 和 6105 的最大公约数 求 225 和 135 的最大公约数

辗转相除法

所谓辗转相除法：

就是对于给定的两个数，用较大的数除以较小的数。

若余数不为零，则将余数和较小的数构成新的一对数，继续上面的除法，直到大数被小 数除尽，则这时较小的数就是原来两个数的最大公约数。

例子

求 8251 和 6105 的最大公约数过程：

第一步： 用两数中较大的数除以较小的数，求得商和余数：

8251=6105 x 1 + 2146

结论：8251 和 6105 的公约数就是 6105 和 2146 的公约数，求 8251 和 6105 的最大公约 数，只要求出 6105 和 2146 的最大公约数就可以了。

第二步：若余数不为零，则将余数和较小的数构成新的一对数，继续上面的除法：

6105 = 2146 x 2 + 1813

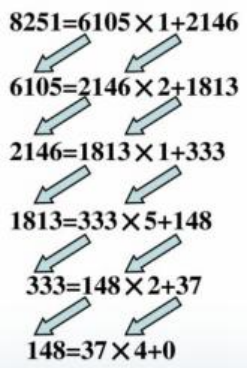
同理：6105 和 2146 的最大公约数就是 2146 和 1813 的最大公约数。

显然 37 是 148 和37 的最大公约数， 也就是 8251 和 6105 的最大公约数

辗转相除法的规律

第一步：用大数除以小数

第二步：除数变成被除数，余数变成除数

第三步：重复第一步，直到余数为 0

辗转相除法编成计算机程序

#include <iostream>
using namespace std; 
int main() {
    int a,b,r;
    cin>>a>>b;
    r=a%b;
    //如果余数为0，则除数b就是最大公因数 
    while(r!=0) {
        a=b;//除数赋值给除数 
        b=r;//余数赋值给除数 
        r=a%b;
    }
    cout<<b<<endl;
    return 0;
}

课后练习

第 1 题: 使用辗转相除法求 123456 和 678 的最大公约数

第 2 题: 使用辗转相除法求 1859 和 1573 的最大公约数