什么是递归
函数的自我调用(直接、间接调用)
直接递归:方法直接自己调用自己
间接递归:用a方法调用b方法,b方法再调用a方法
递归代码最重要的两个特征:结束条件和自我调用。自我调用是在解决子问题,而结束条件定义了最简子问题的答案。
int func(传入数值) {
if (终止条件) return 最小子问题解;
return func(缩小规模);
}
为什么要写递归
1、结构清晰,代码简洁:它能用非常简洁的代码解决一些看起来很复杂的问题。
2、练习分析问题的结构:当发现问题可以被分解成相同结构的小问题时,递归写多了就能敏锐发现这个特点,进而高效解决问题。
2、适用于特定问题:递归特别适用于处理树形结构和图形结构的数据,如树的遍历、图的搜索等。
递归的过程
递归的过程总结起来其实就是6个字:递过去,归回来
递过去:程序不断深入地调用自身,通常传入更小或更简化的参数,直到达到“终止条件”。
大问题向小问题规模缩小的“递”
归回来:触发“终止条件”后,程序从最深层的递归函数开始逐层返回,汇聚每一层的结果。
由小问题的解回归到大问题的解的“归”
递归实际上就是通过栈这种数据结构实现的,递的过程就是入栈的过程,归的过程就是出栈的过程,后入先出,最后入栈的最内层函数,不断出栈计算结果形成递归。
模型一:在递去的过程中解决问题
返回值 func(大规模){
if (终止条件){ // 明确的递归终止条件
return 最小子问题的解;
}
solve; //解决问题
func(小规模); // 递去,在将问题转换为子问题的每一步,解决该步中剩余部分的问题
}
模型二: 在归来的过程中解决问题
返回值 func(大规模){
if (终止条件){ // 明确的递归终止条件
return 最小子问题的解;
}
func(小规模); // 递去,在将问题转换为子问题的每一步,解决该步中剩余部分的问题
solve; //归来,解决问题
}
正向输出1-100
void f(int x){
if(x>100) return;
cout<<x<<" ";//打印数字
f(x+1); //递进去
}
int main() {
f(1);
return 0;
}
逆向输出1-100
void f(int x){
if(x>100) return;
cout<<x<<" ";//正向打印数字
f(x+1); //递进去
cout<<x<<" ";//归回来 逆向打印数字
}
int main() {
f(1);
return 0;
}
累加求和
int fun(int x){
if(x==1)
return 1;
return x+fun(x-1);
}

- 计算sum(5)时,先sum(5)入栈,然后原问题sum(5)拆分为子问题sum(4),再入栈,直到终止条件sum(n=1)=1,就开始出栈。
- sum(1)出栈后,sum(2)开始出栈,接着sum(3)。
- 最后呢,sum(1)就是后进先出,sum(5)是先进后出,因此递归过程可以理解为栈出入过程。
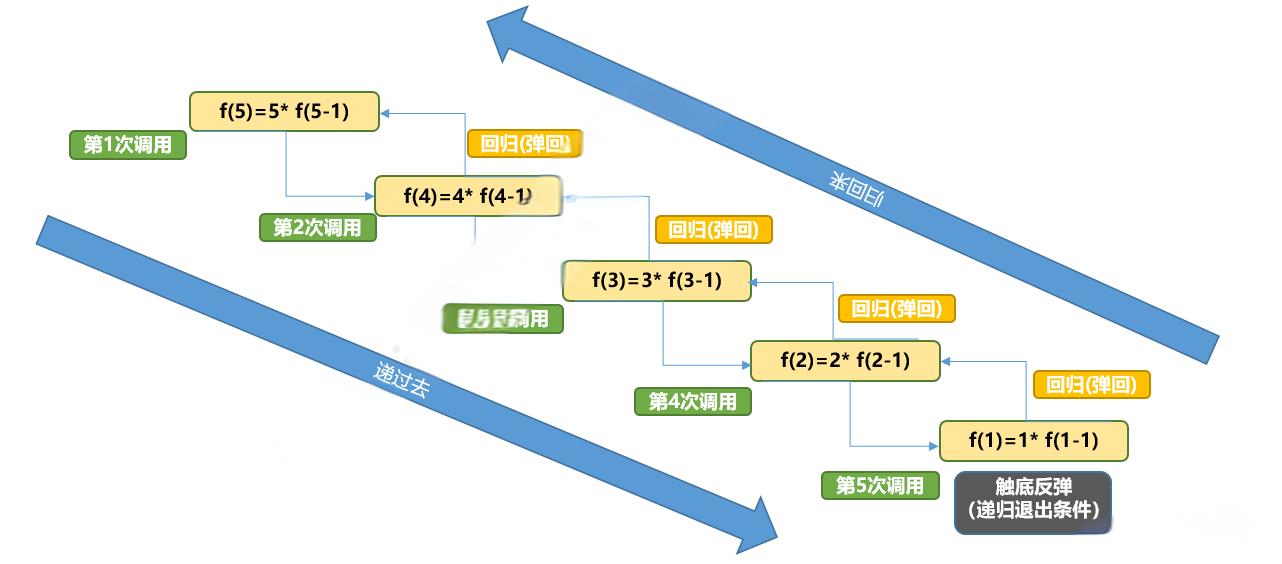
计算阶乘
long long f(int n){
if(n==0) return 1;
return n*f(n-1);
}
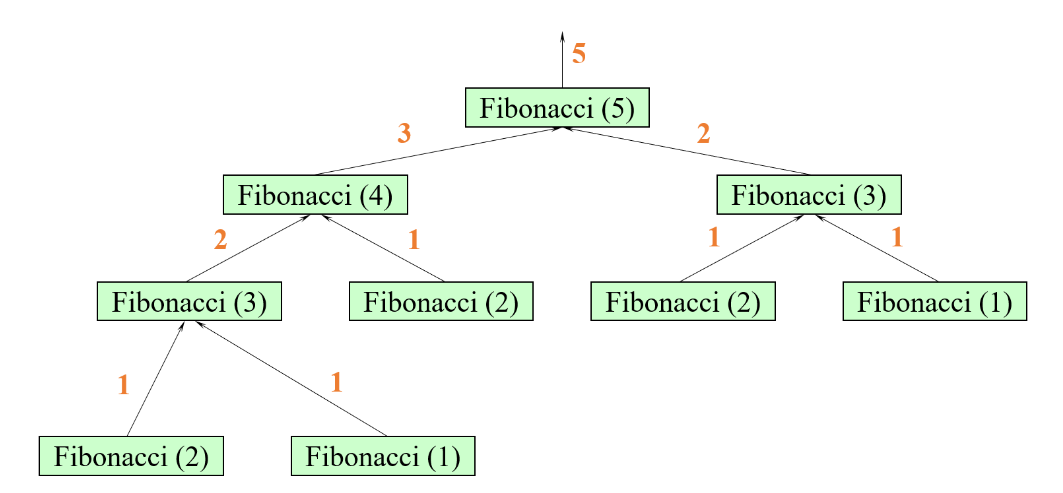
斐波那契数列
int f(int x){
if(x==1) return 0;
if(x==2) return 1;
return f(x-1)+f(x-2);
}
从实现的角度看,递归代码主要包含以下几个知识点:
- 递归终止条件: 递归终止条件是指确定递归何时停止的条件。递归函数在执行时,检查是否满足终止条件,如果满足,则直接返回一个结果,结束递归。
- 递归调用: 在递归函数内部,需要调用自身来解决规模较小的子问题。递归调用的目的是将原始问题划分为多个具有相同结构的子问题。
- 问题规模更新: 在进行递归调用时,需要更新问题的规模,使得每次递归调用的问题规模越来越小。该更新可以通过传递参数,在递归调用中改变参数的数值。
- 问题结果处理: 在递归终止条件满足时,需要处理问题的结果并返回。这可能涉及对递归返回的结果进行操作,或者将多个子问题的结果合并。
如何写递归
写递归,就是写三要素的实现,三要素分别为函数,边界,递推公式
递归首要元素-函数
明确你的函数是干什么用的,函数的入参应该是什么,返回值是什么
递归边界、跳出递归
递归就是有去有回,既然这样,那么必然应该有一个明确的临界点,程序一旦到达了这个临界点,就不用继续往下递去而是开始实实在在的归来。如果递归没有终止,操作系统的内存栈必然就会溢出。
递归的结束条件通常是最小子问题的答案
递归公式
递归问题必须可以分解为若干个规模较小、与原问题形式相同的子问题,这些子问题可以用相同的解题思路来解决。从程序实现的角度而言,我们需要抽象出一个干净利落的重复的逻辑,以便使用相同的方式解决子问题。
提取重复的逻辑,缩小问题规模
递归的复杂度分析
递归函数每次调用自身时,系统都会为新开启的函数分配内存,以存储局部变量、调用地址和其他信息等。
- 函数的上下文数据都存储在称为“栈空间”的内存区域中,直至函数返回后才会被释放。因此,递归通常比迭代更加耗费内存空间。
- 递归调用函数会产生额外的开销。因此递归通常比循环的时间效率更低。
- 递归的深度过大可能会导致栈溢出。所以根据问题规模和具体需求来选择使用迭代还是递归,两者都有各自的适用场景。
迭代vs递归
迭代就是流水线打螺丝,重复干一件相同的事。
| 迭代 | 递归 | |
|---|---|---|
| 实现方式 | 循环结构 | 函数调用自身 |
| 时间效率 | 效率通常较高,无函数调用开销 | 每次函数调用都会产生开销 |
| 内存使用 | 通常使用固定大小的内存空间 | 累积函数调用可能使用大量的栈空间 |
| 适用问题 | 适用于简单循环任务,代码直观、可读性好 | 适用于子问题分解,如树、图、分治、回溯,快速排序和归并排序等,代码结构简洁、清晰 |
从计算角度看,迭代与递归可以得到相同的结果,但它们代表了两种完全不同的思考和解决问题的范式。
- 迭代:“自下而上”地解决问题。从最基础的步骤开始,然后不断重复或累加这些步骤,直到任务完成。
- 递归:“自上而下”地解决问题。将原问题分解为更小的子问题,这些子问题和原问题具有相同的形式。接下来将子问题继续分解为更小的子问题,直到基本情况时停止(基本情况的解是已知的)。
递归进阶
在基础语法阶段,我们讲解的递归基本是给出数学推导式,更进一步,我们需要根据问题,判断是否应该使用递归解决。
如果确定需要递归解决,如何划分问题规模,使每一个递归过程都是独立的,问题规模向递减趋势发展,且有终止值。
且在递归过程中可能会出现大量重复计算,例如我们在基础语法阶段讲解过的递归求斐波那契数列,这个时候就可以使用记忆化存储,也叫做数组暂存优化,就是利用一个辅助数组T将计算过的结果保存起来,之后遇到$F_i$的值在数组中存储过,就直接使用T[i]的值,不需要继续递归计算。
例题:汉诺塔问题
题目描述
约19世纪末,在欧州的商店中出售一种智力玩具,在一块铜板上有三根杆,最左边的杆上自上而下、由小到大顺序串着由64个圆盘构成的塔。目的是将最左边杆上的盘全部移到中间的杆上,条件是一次只能移动一个盘,且不允许大盘放在小盘的上面。
这是一个著名的问题,几乎所有的教材上都有这个问题。由于条件是一次只能移动一个盘,且不允许大盘放在小盘上面,所以64个盘的移动次数是:18,446,744,073,709,551,615
这是一个天文数字,若每一微秒可能计算(并不输出)一次移动,那么也需要几乎一百万年。我们仅能找出问题的解决方法并解决较小N值时的汉诺塔,但很难用计算机解决64层的汉诺塔。
假定圆盘从小到大编号为1, 2, ...
输入
输入为一个整数(小于20)后面跟三个单字符字符串。
整数为盘子的数目,后三个字符表示三个杆子的编号。
输出
输出每一步移动盘子的记录。一次移动一行。
每次移动的记录为例如 a->3->b 的形式,即把编号为3的盘子从a杆移至b杆。
样例
2 a b c
a->1->c
a->2->b
c->1->b
解析:
那么如何把N个盘片从A柱移到B柱呢?
1.把上面的N-1个盘片从A移动到C
2.把第N个盘片从A移动到B
3.把上面的N-1个盘片从C移动到B
对于递归的题目来说,我们不需要也没有办法完全思考清楚每一步是怎么做的,但是根据规律,每一层递归所做的事,是完全一样,那也就是说,只要保证了第一层的代码是完全正确的,那么整个递归就是完全正确的,汉诺塔就是个很好的例子。
同时我们也需要注意到,对于递归来说可以把每一次递归看作是个阶段,如何选取递归的参数,可以参考表示阶段的变量。
如汉诺塔中第一个能想到的变量就是金片个数N,每个阶段的金片个数都会减一,是非常适合做参数的变量之一。