整除的定义

设 $a,b$ 是两个整数，且 $a \neq 0$ , 如果存在一个整数 $c$ ，使得 $b=c \times a$ , 那么就说 $b$ 可以被 $a$ 整

除，记做 $a|b$ 。且称 b 是 a 的倍数，a 是 b 的约数(也称作因数)。

$6 = 2 \times 3$ ， $6$ 是 $3$ 的倍数， $3$ 是 $6$ 的约数(因数) 。

质数

一个数除了 $1$ 和它本身，不再有别的约数，这个数就叫做质数。它是一个独立存在的数。

比如 $17$ 是质数，因为它只有 $1$ 和 $17$ 两个约数。质数只有两个约数(因数)。

一个数除了 $1$ 和它本身，还有别的约数，这个数就叫做合数。

比如 $12$ 是合数，因为除了 $1$ 和 $12$ 两个约数之外，还有 $2$ ， $3$ ， $4$ ， $6$ 这些约数。合数最少有

$3$ 个约数。

每个大于 1 的整数都可以唯一地分解为有限个质因数的乘积。这意味着一个整数可以表示为若干个质数的乘积，并且这种分解方式是唯一的。例如，12 可以分解为 $2 \times 2 \times 3$ ，这种分解方式是唯一的。

每个合数都可以写成几个质数相乘的形式，其中每个质数都是这个合数的因数（约数），叫做这个合数的质因数。

质因数既是质数，也是因数。

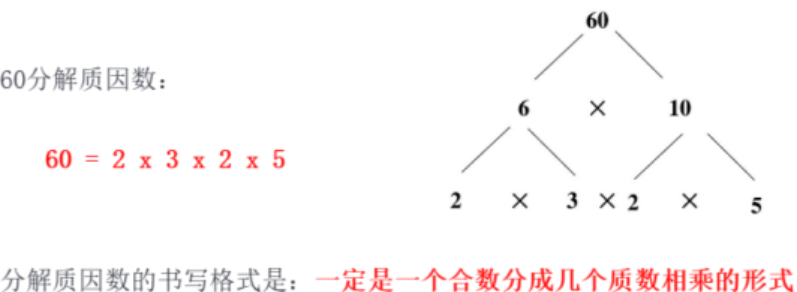
把一个合数用质因数相乘的形式表示出来，叫做分解质因数。

是指将一个合数（非质数）分解为若干个质因数的乘积。例如，将 6 分解为 2

和 3 的乘积，即 $6 = 2 \times 3$ 。

分解质因数的方法

短除法: 从最小的质数 2 开始，逐个尝试能否整除目标数，如果能整除，则继续除以该

质数，直到不能再整除为止。

把一个合数分解质因数，先用一个能整除这个合数的质数（通常从最小的开始）去除：

得出的商如果是质数，就把除数和商写成相乘的形式；

得出的商如果是合数，就按照上面的方法继续除下去，直到得出的商是质数为止；

最后把各个除数和最后的商写成相乘的形式。

第 1 题: 12 分解质因数 = （）

第 2 题: 24 分解质因数 = （）

第 3 题: 35 分解质因数 = （）

第 4 题: 54 分解质因数 = （）

第 5 题: 56 分解质因数 = （）�� ）