引入

如图,由 A 村去 B 村的道路有 3 条，由 B 村去 C 村的道路有 2 条。从 A 村经 B 村去 C 村，共有多少种不同的走法?

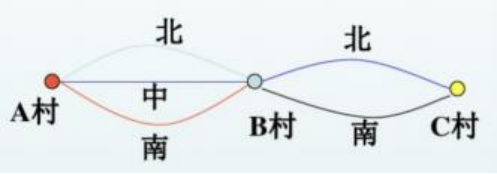
解题思路： 从 A 村北出发有两种选择（B 村北、B 村南），同理，A 村中和 A 村南也是两种。

所以总次数为 3*2=6 种

乘法原理

做一件事情，完成它可以有 $n$ 个步骤，做第一步时有$m_1$种不同的方法，在第二步时中有$m_2$种不同的方法，……，做第 $n$ 步时有$m_n$种不同的方法。那么完成这件事共有

$N$=$m_1 \times m_2 \times m_3 \times \cdots \times m_n$ 种不同的方法

即完成一件事情，需要分为几个步骤，每个步骤内的方法刚好完成该步骤，所有步骤实施完毕刚好完成这件事，则完成这件事情的方法总数等于每一个步骤的方法数之积。乘法原理是“分步完成”

【举例说明】从 A 地到 B 地需在 C 地转机，已知从 A 地到 C 地有 4 种方法，从 C 地到 B 地有

3 种方法。那么从 A 地到 B 地要分两步，A→C、C→B，共有 4x3=12 种方法。

练习

1、由数字 1，2，3，4，5 可以组成多少个允许有重复数字的三位数?

2、书架的第一层放有 4 本不同的计算机书, 第二层放有 3 本不同的文艺书, 第三层放有 2 本不同的体育书。从书架的第一、二、三层各取一本书，有多少种不同的取法?

3、甲班有 10 人，乙班有 8 人，丙班有 5 人，各选出一人当班代，请有几种不同的结果?

4、从 A 地到 B 地, 要先到 C 地。A 到 C 有 5 趟火车, C 到 B 有8 趟轮船可以选。请问 A 地到 B 地共有几趟交通工 具?

5、小明去食堂买饭，有 3 样主食，5 样菜。小明要买一份主食一份菜，共有多少种不同的买法？