进制转换

进制也就是进位计数制，是人为定义的带进位的计数方法。对于任何一种进制 X进制， 就表示每一位置上的数运算时都是逢 X 进一位。 十进制是逢十进一，十六进制是逢十六进 一，二进制就是逢二进一，以此类推， X 进制就是逢 X 进位。

数制：是用一组固定的符号和统一的规则来表示数值的方法。

数码：数制中表示基本数值大小的不同数字符号。

基数：数制所使用数码的个数。

位权：数制中某一位上的1所表示数值的大小。

例：123中，1的位权是100，2的位权是10，3的位权是1

按位权展开：把数字写成数码乘位权的加和形式

123 = 1*100 + 2*10 + 3

区别不同进制数字的记法：$(1101)_2$ $(703)_8$ $(5F)_16$

对于任意进制来说（比如R进制）

①R进制即要求满R进一

②R进制下的数每一数位都不超过R，即每一数位的范围都是0∼R−1

③R进制从最低位到最高位，数位的权值分别为：R0,R1,R2,R3...

二进制

二进制 Binary （简写：B）

数码：0、1

基数：2

例：

$(101)_2=1\ast2^2+0\ast2^1+1\ast2^0=(5)_{10}$

$(1101)_2=1\ast2^3+1\ast2^2+0\ast2^1+1\ast2^0=(13)_{10}$

八进制

八进制 Octal （简写：O，Oct）

数码：0、1、2、3、4、5、6、7

基数：8

例：

$(15)_8=1\ast8^1+5\ast8^0=(13)_10$

$(101)_8=1\ast8^2+0\ast8^1+1\ast8^0=(65)_10$

十进制

十进制 Decimal （简写：D，Dec）

数码：0、1、2、3、4、5、6、7、8、9

基数：10

例：

$(1234)_{10}=1\ast10^3+2\ast10^2+3\ast10^1+4\ast10^0$

$(101)_{10}=1\ast10^2+0\ast10^1+1\ast10^0$

十六进制

十六进制 Hexadecimal （简写：H，Hex, x）

数码：0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F

基数：16

例：

$(3F)_{16}=3\ast16^1+15\ast16^0=(63)_{10}$

$(101)_{16}=1\ast16^2+0\ast16^1+1\ast16^0=(257)_{10}$

二进制、八进制、十六进制的关系

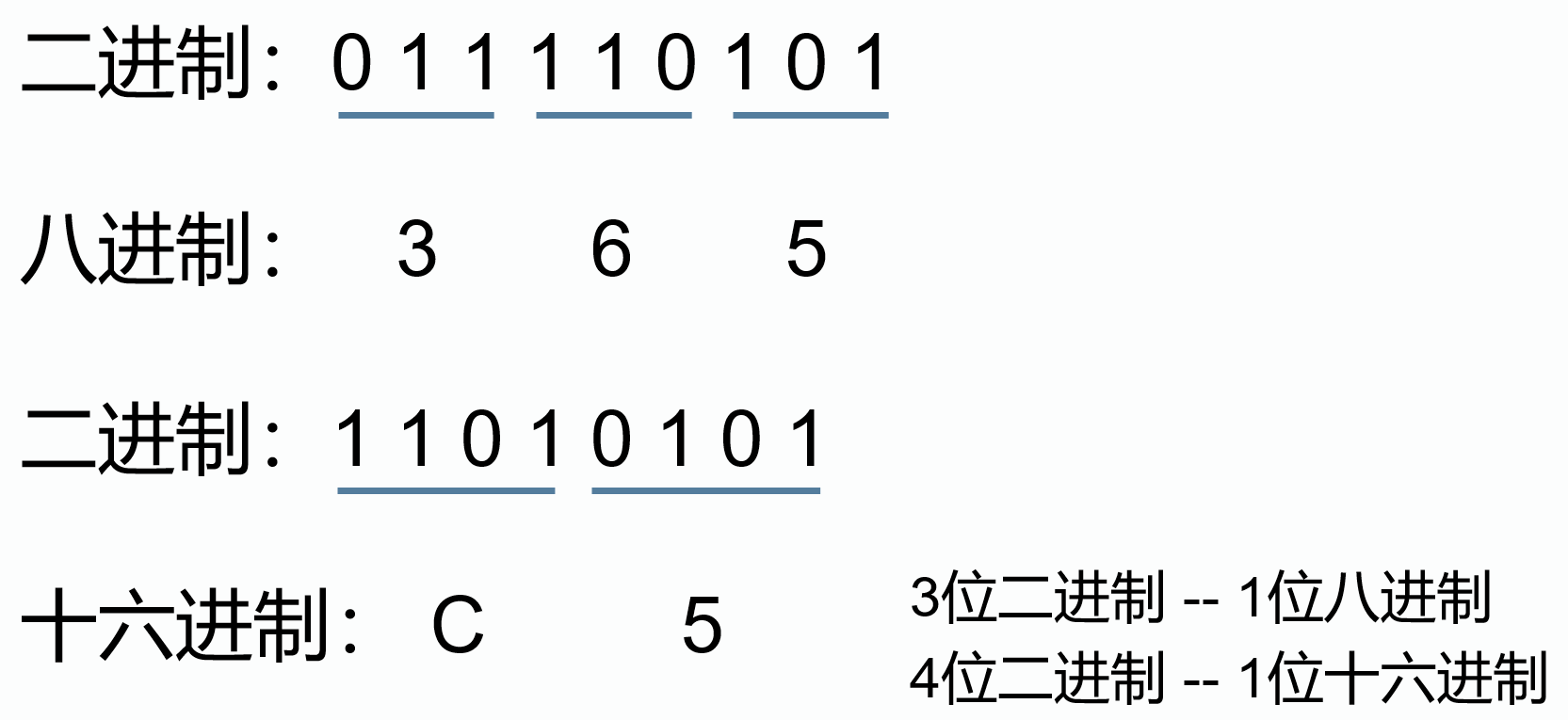
R进制数字串转为十进制

按位权展开求和：即把每一个数位数字乘以对应权值相加

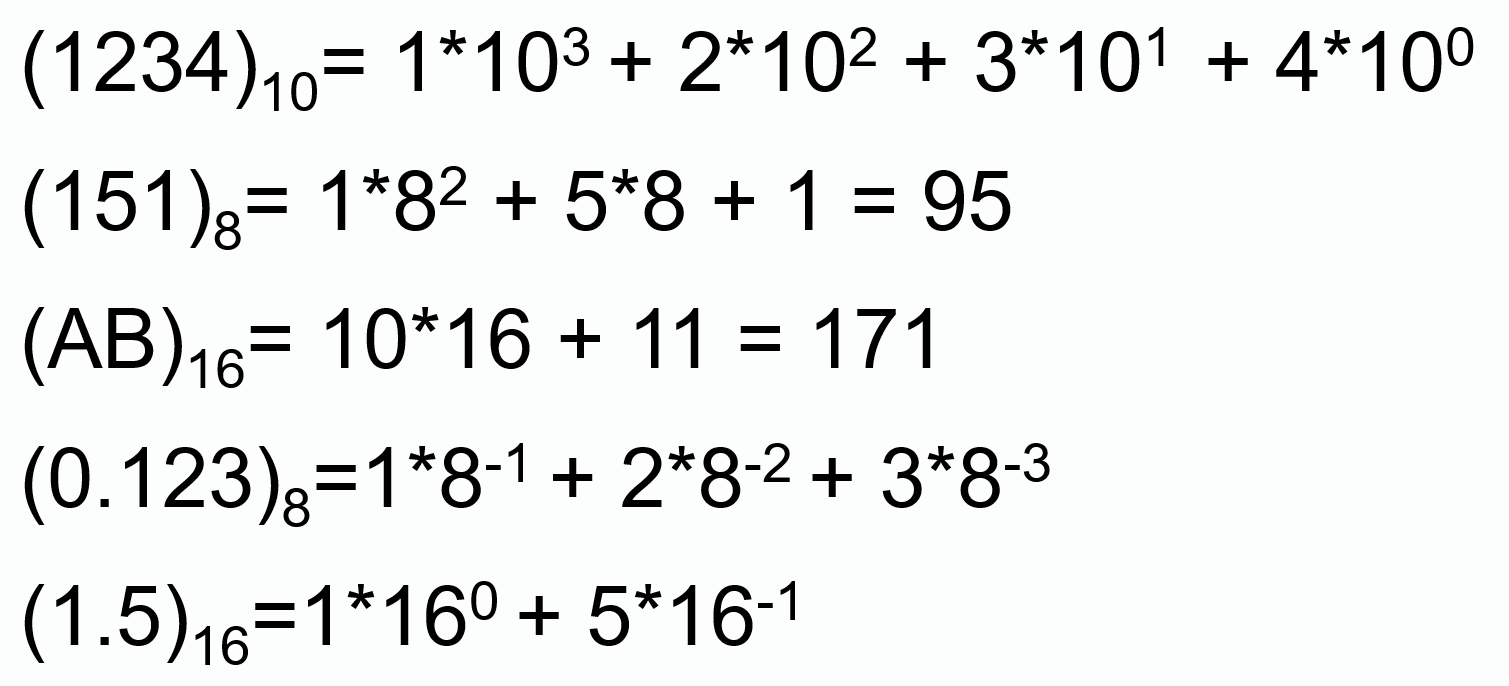
十进制整数转R进制

除R反向取余法：即把除以R的商进位、留下余数

代码实现

#include<bits/stdc++.h>
using namespace std;
//二进制转成十进制,按权展开求和
int main()
{
    int n,num=0;
    string b;
    cin>>n>>b;
    for(int i=1;i<=n;i++){
        int a=b[n-i]-'0';//转成数字，系数 
        num+=a*pow(2,i-1);
    }
    cout<<num;
    return 0;
 }

信息编码

机器数

一个数在计算机中的二进制表示形式, 叫做这个数的机器数。

有符号机器数的最高位为符号位，0 表示正数，1 表示负数。

将带符号位的机器数对应的真正数值称为机器数的真值。

真值：3 机器数：0000 0011

真值：-3 机器数：1000 0011

原码反码补码

原码：符号位加上真值, 即用第一位表示符号, 其余位表示值。

反码：

• 正数的反码与原码相同
• 负数的反码：符号位不变，其余各位取反

补码：

• 正数的补码与原码相同
• 负数的补码：反码加 1