五级考纲
- 初等数论
- 素数表的埃氏筛法和线性筛法
- 数组模拟高精度加法、减法、乘法、除法
- 单链表、双链表、循环链表
- 二分查找/二分答案(也称二分枚举法)
- 贪心算法
- 递归算法
- 分治算法(归并排序和快速排序)
- 算法复杂度的估算(含多项式、指数、对数复杂度)
知识点解析
一.初等数论
约数、倍数、素数、合数
约数:如果一个整数 a 除以另一个非零整数 b,商为整数,且余数为零,我们就说 b 是 a 的约数。
- 约数也叫因数。
- 一个数的约数总是成对出现的(除了完全平方数,其平方根只出现一次)。
- 例子:6 的约数有 1、2、3 和 6,因为 6 可以被这些数整除。
倍数:如果 a 和 b 都是整数,且 b 不是 0,那么 a 是 b 的倍数当且仅当 a 除以 b 的余数为 0。
- 一个数的倍数是无限多的,除非这个数是 0(0 没有正倍数)。
- 任何数都是 1 和它本身的倍数。
- 例子:3 的倍数有 3、6、9、12、15 等,因为这些都是 3 的整数倍。
素数(质数):一个大于 1 的自然数,除了 1 和它自身外,无法被其他自然数整除的数叫做素数。
- 素数只有两个正因数:1 和它自己。
- 最小的素数是 2。
- 例子:2、3、5、7、11、13、17、19 等都是素数。
合数:除了 1 和它本身以外还有其他因数的数叫做合数。
- 合数至少有三个正因数。
- 例子:4、6、8、9、10、12 等都是合数(因为它们除了 1 和自己外,还有其他因数)。
//判断质数,任何一个合数都可以表示为两个整数的乘积,小因数和大因数,小因数的最大值是这个数的平方根
bool isPrime(int n){
if(n < 2) return false;
for(int i = 2; i <= n / i; i++){
if(n % i == 0)
return false;
}
return true;
}
最大公约数与最小公倍数
最大公约数:设 a1 和 a2 是两个整数,如果 a1 能被 d 整除,a2 也能被 d 整除,那么 d 就被称为 a1 和 a2 的公约数。其中最大的称为 a1 和 a2 的最大公约数。
greatest common divisor,简写为 gcd
数学方法:求几个数的最大公约数,先把这些数分解质因数,再将质因数的公共部分相乘即可。
例如:求 12 和 18 的最大公约数?
12 = 2 × 2 × 3 18 = 2 × 3 × 3
质因数 2,3 是 12 和 18 这两个数共有的,所以 2x3(质因数的乘积)就是 12 和 18 的最大公 约数。
当gcd=1时,成为两个数互质
最小公倍数:设 a1 和 a2 是两个整数,如果 d 能被 a1 整除,d 也能被 a2 整除,那么 d 就被称为 a1 和 a2 的公倍数。其中最小的称为 a1 和 a2 的最小公倍数。
Least Common Multiple,简称lcm
数学方法:最小公倍数等于它们所有的质因数的乘积(如果有几个质因数相同,则乘于两个数当中拥有 更多的质因数的次数)
例如:求 18 和 27 的最小公倍数?
18 = 2 × 3 × 3 27 = 3 × 3 × 3
最小公倍数 = 2 × 3 × 3 × 3 = 54
辗转相除法(也称欧几里得算法)
就是对于给定的两个数,用较大的数除以较小的数。
若余数不为零,则将余数和较小的数构成新的一对数,继续上面的除法,直到大数被小 数除尽,则这时较小的数就是原来两个数的最大公约数。
求 8251 和 6105 的最大公约数过程:
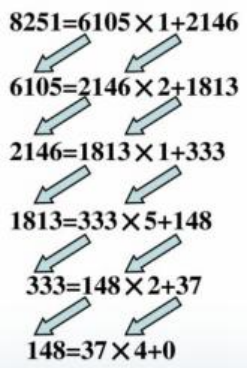
第一步:用大数除以小数
第二步:除数变成被除数,余数变成除数
第三步:重复第一步,直到余数为 0
#include <iostream>
using namespace std;
int main() {
int a,b,r;
cin>>a>>b;
r=a%b;
//如果余数为0,则除数b就是最大公因数
while(r!=0) {
a=b;//除数赋值给除数
b=r;//余数赋值给除数
r=a%b;
}
cout<<b<<endl;
return 0;
}
int gcd(int x,int y){
return y==x?x:gcd(y,x%y);
}
两个数最小公倍数的求法
定理:a,b的最大公约数乘以最小公倍数等于a和b本身的乘积。
唯一分解定理
每个大于 1 的整数都可以唯一地分解为有限个质因数的乘积。这意味着 一个整数可以表示为若干个质数的乘积,并且这种分解方式是唯一的。例如,$12$ 可以分解 为 ,这种分解方式是唯一的。
分解质因数
每个合数都可以写成几个质数相乘的形式,其中每个质数都是这个合数的因数(约数),叫 做这个合数的质因数。
质因数既是质数,也是因数。
把一个合数用质因数相乘的形式表示出来,叫做分解质因数。
是指将一个合数(非质数)分解为若干个质因数的乘积。例如,将 6 分解为 2
和 3 的乘积,即 。
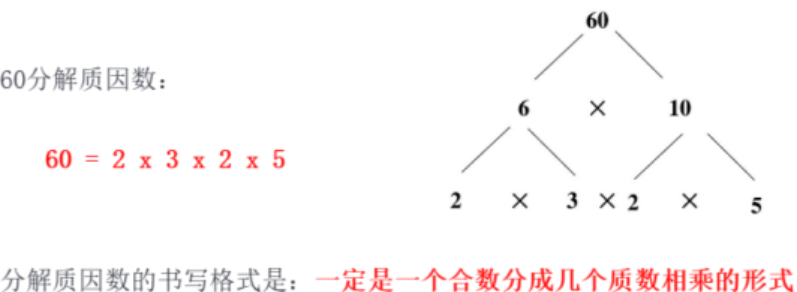
//36=2^2 * 3^2
void splitInt(int n){
int flag=1;
for(int i=2; i<=n; i++) {
int cnt=0;
while(n%i==0) { //整除干净
cnt++;
n/=i;
}
if(cnt>0) {
if(flag==1) flag=0;
else cout<<"* ";
if(cnt==1) cout<<i<<" ";
else cout<<i<<"^"<<cnt<<" ";
}
}
}
模运算与同余
模运算:表示两个整数相除所得的余数。模运算的符号是 mod,C++模运算符%。
- 带余除数 a ÷ b = q…r, 也等价于 a mod b = r
- 例如:13 mod 4 = 1 (13 除以 4 的商是 3,余数是 1)
- 同余:若整数 a、b 同除以自然数 n 的余数相同,则称 a 和 b 对模 n 同余。
- 记作 a ≡ b (mod n) 。 “≡”读作同余。
- 27 和 51 同除以 8,余数都是 3。 记作 27 ≡ 51 (mod 8)
- 余数定理
- 加法:(a + b)%m = (a%m + b%m)%m
- 减法:(a - b)%m = (a%m - b%m+m)%m
- 乘法:(axb)%m = (a%mxb%m) %m
二.质数筛法
埃式筛法:只有质数才可能标记后面的合数。

int book[1005];
void get_primes(int n){//埃式筛
memset(book,1,sizeof(book));//默认都是质数
for(int i=2;i<=n/i;i++){//从最小的质数2开始
if(book[i]){
for(int j=2*i;j<=n;j+=i)
book[j]=0;//质数的倍数标记为合数
}
}
}
欧拉筛法:(线性筛法)设 的最小质因数为 ,则 只会被 标记。
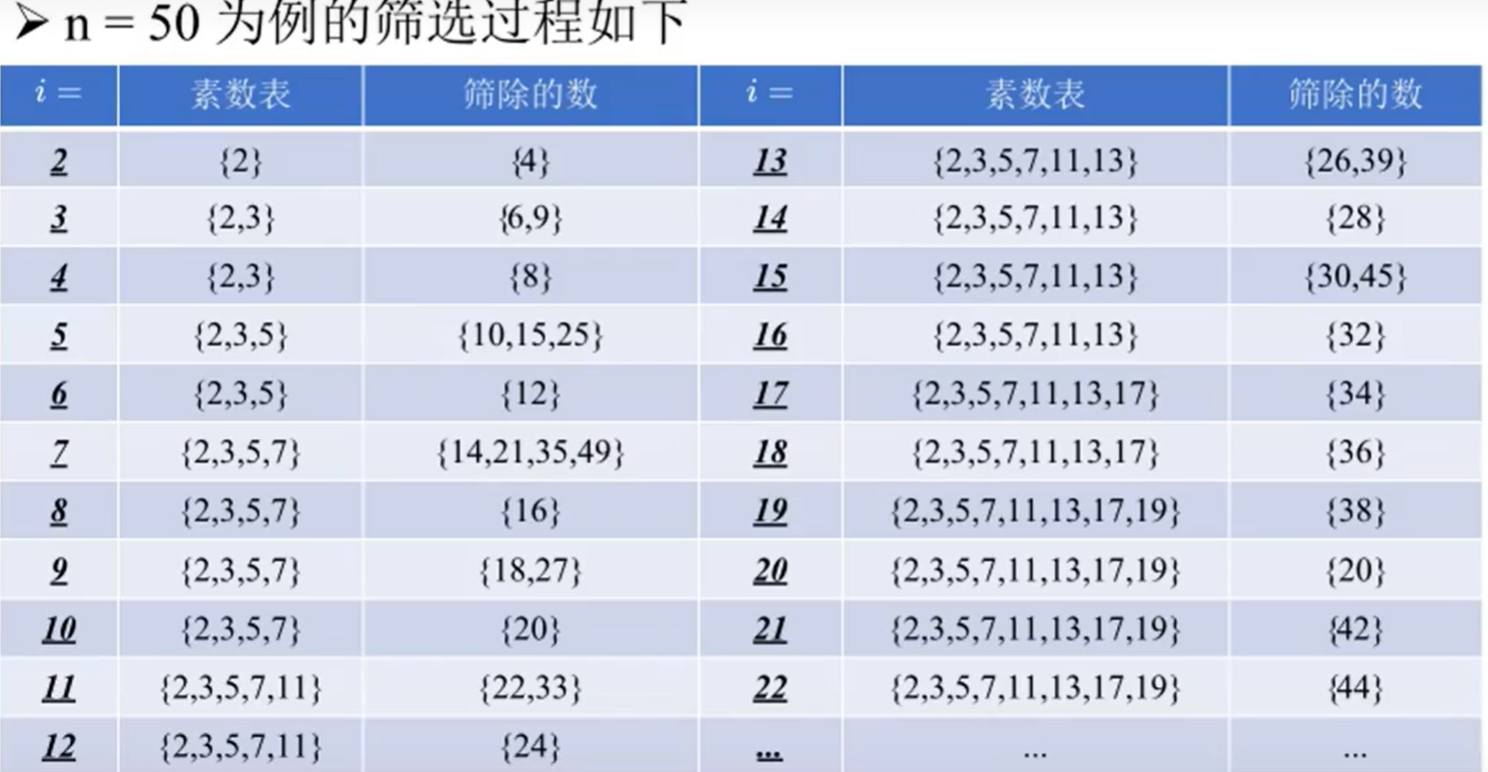
int book[1005],p[1005],cnt;
void get_primes(int n){ //欧拉筛
memset(book,1,sizeof(book));//默认都是质数
for(int i=2;i<=n;i++){
if(book[i])
p[++cnt]=i;//如果是质数,则存进质数表
//循环质数表
for(int j=1;j<=cnt&&i*p[j]<=n;j++){//i*p[j]<=n 防止数组越界
book[i*p[j]]=0; //最小质因数的才被筛掉
//判断是否能被最小质因数整除,确保每个数只被它的最小质因数筛除
if(i%p[j]==0)
break;
}
}
}
三.高精度运算
高精度运算,是指参与运算的数(加数、减数、因子......)范围超过了标准数据类型(整型、实数)能表示的范围的运算。
算法思想:竖式计算模拟高精度
算法过程:
- 1.高精度数的存储,字符串接收数据
- 2.倒序存储在整型数组中,转成数字,数位对齐
- 3.模拟竖式计算,处理进位
- 4.去除前导0
- 5.逆序输出结果
高精度加法
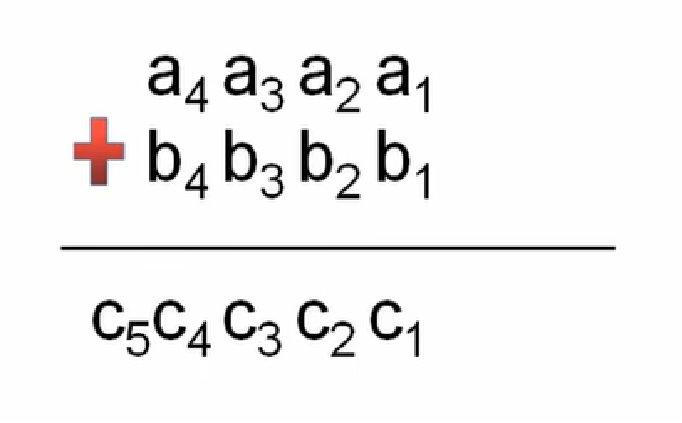
#include<iostream>
using namespace std;
int a[201],b[201],c[201];
int main(){
//输入数据
string s1,s2;
cin>>s1>>s2;
//整型数据 逆序存储
for(int i=0;i<s1.size();i++){
a[i+1]=s1[s1.size()-1-i]-'0';
}
for(int i=0;i<s2.size();i++){
b[i+1]=s2[s2.size()-1-i]-'0';
}
//模拟竖式计算
int lenc=max(s1.size(),s2.size())+1;
for(int i=1;i<=lenc;i++){
c[i]+=a[i]+b[i];
if(c[i]>9){
c[i+1]++;//进位
c[i]=c[i]%10;
}
}
//去掉前导0
while(c[lenc]==0&&lenc>1)
lenc--;
//输出结果
for(int i=lenc;i>=1;i--){
cout<<c[i];
}
return 0;
}
高精度减法
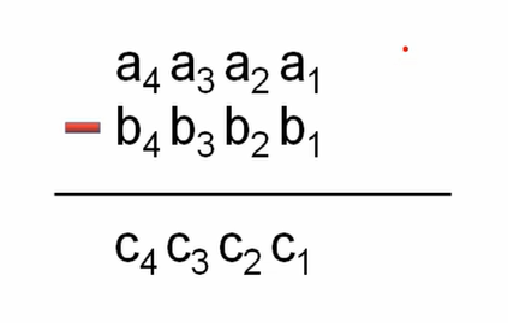
//模拟竖式计算 核心代码
int lenc=max(s1.size(),s2.size());
for(int i=1;i<=lenc;i++){
if(a[i]<b[i]){
a[i+1]--;//借一位
a[i]+=10;
}
c[i]=a[i]-b[i];
}
高精度乘法

//第三步,模拟竖式计算,双层循环,先相乘后累加
//乘法结果的最大位数是两个运算数之和
int lenc=s1.size()+s2.size();
for(int i=1;i<=s1.size();i++){
for(int j=1;j<=s2.size();j++){
c[i+j-1]+=a[i]*b[j];
}
}
//第四步,统一处理进位
for(int i=1;i<=lenc;i++){
if(c[i]>=10){
c[i+1]+=c[i]/10;
c[i]=c[i]%10;
}
}
高精度除法

#include <bits/stdc++.h>
using namespace std;
/*
1、正序存储,因为除法是从高位开始
2、试除法
余数*10+下一位上的数字 除数 更新余数
3、去掉前导0,前导0是在前面
*/
int a[101],c[101],r;
int main(){
string s;
cin>>s;
int lenc=s.size();
//转存到整型数组
for(int i=1;i<=lenc;i++){
a[i]=s[i-1]-'0';
}
//逐位试除
for(int i=1;i<=lenc;i++){
c[i]=(r*10+a[i])/13;
r=(r*10+a[i])%13;
}
//前导0在前面
int i=1;
while(c[i]==0)
i++;
//输出结果
for(;i<=lenc;i++){
cout<<c[i];
}cout<<endl;
cout<<r;
return 0;
}
四.链表
链表相较于数组,可以充分利用内存中分散的空间,每个节点都至少需要一个指针。
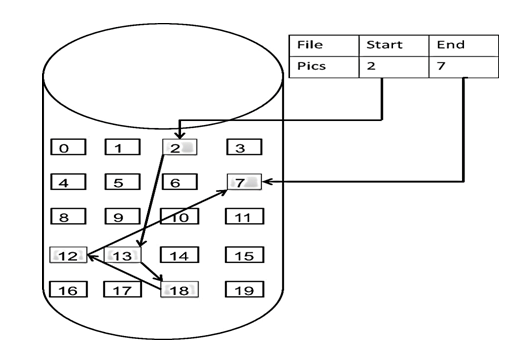
链表是一种通过指针串联在一起的线性结构
单链表
每一个结点点由两部分组成,一个是数据域(data)、一个是指针域(存放指向下一个节点的指针)next,最后一个节点的指针域指向null(空指针的意思)。

- 在链表的第一个结点之前附设一个结点,头指针指向头结点。设置头结点的目的是统一空表与非空表的操作,简化链表操作的实现。
- 第一个结点:链表中存储线性表中第一个数据元素的结点
单链表的操作
struct node{ int data; //存数据 node *next;//存下一个数据点的地址 };创建
- 不带头结点
node *head=NULL;带头结点
node *head; head =new(node); head->next=NULL;
输出
//定义指针p,先指向第一个元素,如果该结点存在,则输出并向后移动 p=head->next; while(p!=NULL){ cout<<p->data<<" "; p=p->next; }插入
- 头插法
//设p为要插入的结点指针 p->next=head->next; head->next=p;- 尾插法
//设p为要插入的结点指针,设一个尾指针tail始终指向链表最后一个结点。 tail->next=p; tail=p;- 插入某结点之后
//设p为要插入的结点指针,将结点p插入链表中q结点后面 p->next=q->next; q->next=p;删除
//设p为要删除的结点指针,q为p的前驱结点 q->next=p->next; delete(p);查找
//查找关键字为key的结点 p=head->next; while(p!=NULL&&p->data!=key){ p=p->next; } //P为NULL则没有找到
双链表
单链表中的指针域只能指向节点的下一个节点。
双链表:每一个节点有两个指针域,一个指向下一个节点,一个指向上一个节点。
双链表 既可以向前查询也可以向后查询,在需要频繁访问前驱和后继结点的时候,使用双向链表。

struct dnode{ int data;//数据项 dnode *prev;//前驱指针 dnode *next;//后继指针 };插入
//在p结点后插入s结点 bool insertnode(dnode *p,dnode *s){ if(p==NULL||S==NULL) return false; s->next=p->next; if(p->next!=NULL) p->next->prev=s; s->prev=p; p->next=s; return true; }删除
bool delnode(dnode *p){ if(p==NULL) return false;//p为空 dnode *q=p->next; if(q==NULL) return false;//p没有后继结点 p->next-q->next; if(q->next!=NULL) p->next->prev=p; delete(q); return true; }
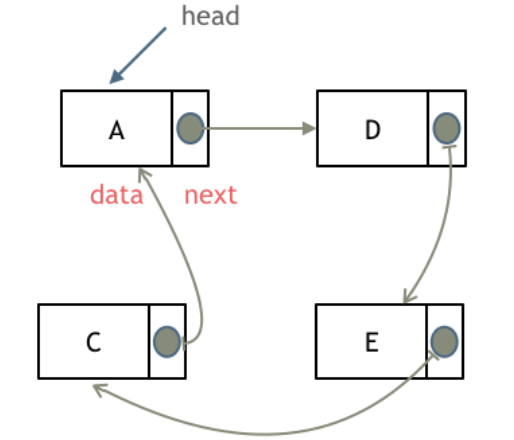
循环链表
将链表中最后一个结点的next域指向头结点,首尾相连,就是循环链表。
循环链表可以用来解决约瑟夫环问题。
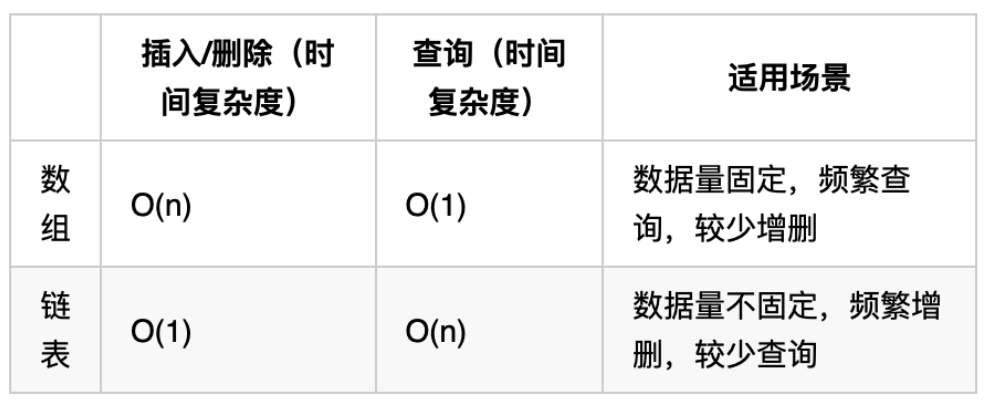
顺序存储与链式存储结构比较
五.二分
二分查找
二分查找,也称折半搜索,是用来在一个有序数组中查找某一元素的算法。
二分思想
- 二分查找要求搜索的区间是有序的;
- 二分查找是通过不断缩小解可能存在的范围,从而求得问题最优解的方法;
- 二分查找每一次检查范围的中点,从而确定答案的位置在中点的左边还是右边,这样每次就能把问题的可能存在范围缩小一半;
基本代码模板
int binarysearch(int a[],int n) { int l=1,r=n,ans=-1;//保存答案 while(l<=r) { int mid=(l+r)/2; if(a[mid]==x) { ans=mid;//更新答案 break; } else if(a[mid]>x) { //前半段 r=mid-1; } else if(a[mid]<x) { //后半段 l=mid+1; } } return ans; }二分答案
使用场景:要求我们求出某变量在满足某种条件下的最大值或最小值。
使用前提:
- 答案在一个固定的区间内
- 难以通过搜索来找到符合要求的值,但给定一个值你可以很快的判断它是不是符合要求
- 可行解对于区间要符合单调性
求满足某个条件的最大值(最小值最大化)
//验证答案是否正确 bool check(int x){ //根据具体问题写验证逻辑 } int main() { ....//输入数据 int l=1,r=n,mid,ans=-1; while(l<=r){ mid=(l+r)/2; if(check(mid)){ ans=mid; l=mid+1;//调整上限,看能不能更大,到后半段去找 }else{ r=mid-1; } } //输出 ans return 0; }求满足某个条件的最小值(最大值最小化)
//验证答案是否正确 bool check(int x){ //根据具体问题写验证逻辑 } int main() { ....//输入数据 int l=1,r=n,mid,ans=-1; while(l<=r){ mid=(l+r)/2; if(check(mid)){ ans=mid; r=mid-1;//调整下限,看能不能更小,到前半段去找 }else{ l=mid+1; } } cout<<ans; return 0; }
六.贪心算法
贪心算法是指在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,只做出在某种意义上的局部最优解。
贪心算法不是对所有的问题都能得到最优解,关键是贪心策略的选择。
无后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。
- 最优子结构,当一个问题的最优解包含子问题的最优解时,称此问题具有最优子结构性质,
七.递归算法
函数的自我调用(直接、间接调用)
递归函数最重要的两个特征:结束条件和自我调用。
- 自我调用是在解决子问题
- 结束条件定义了最简子问题的答案。
int func(传入数值) {
if (终止条件) return 最小子问题解;
return func(缩小规模);
}
递归的特点
- 在时间和空间的开销比较大(缺点)
代码简洁、清晰(优点)
递归的优化策略
递归+记忆化
- 递归分析,递归实现
八.分治算法
分治算法即“分而治之”,有些问题整体求解比较困难或无法求解,但可以将问题分解成两个或多个规模更小相同的子问题,直到子问题规模很小可以直接求解为止,对子问题分别求解后再合并成整个问题的算法。
由于原问题与子问题相同,求解方法类似,分治算法常常是一个递归过程
分治算法的一般过程
- 分:将问题分解成两个或多个规模更小的相同子问题
- 治:分别对子问题求解
- 并:将子问题合并成原问题的解
算法框架
void work(){ if(问题规模较小,不可再分) 直接求解; else{ 分:将问题分解成若干个子问题; 治:对子问题分别求解; 并:将子问题的解合并成问题的解; } }
经典分治算法
快速排序算法
算法思想:通过一趟排序,将序列分成两个部分,其中一部分中所有的数都比另一部分所有数小,通过递归,对两部分分别再进行排序就可以得到有序序列。
时间复杂度:
不稳定
void qsort(int l,int r){ //分,将序列分成两个部分,前一部分比后一部分小 int i=l,j=r; int mid=a[(l+r)/2]; while(i<=j){ while(a[i]<mid) i++; while(a[j]>mid) j--; if(i<=j){ int t=a[i]; a[i]=a[j]; a[j]=t; i++,j--; } } // 治,递归,两部分分别进行排 if(l<j) qsort(l,j); if(i<r) qsort(i,r); // 并,由于在原数组中操作,无序并操作 }
归并排序
算法思想:将要排序的序列均匀地分成两个部分,分别对两部分进行合并排序使之有序,再对两个有序序列进行归并操作,最终完成排序。
时间复杂度:
稳定
void mergeSort(int left,int right) {//排序left到right区间 int mid = (left + right) / 2; if(left >= right) return;//区间不存在或者只有一个元素 就不排序了 mergeSort(left, mid);//先递归左半部分 mergeSort(mid + 1, right);//再递归右半部分 int l = left, r = mid+1, p = 0; while(l <= mid && r <= right) {//在合理的区间比较 if(a[l] <= a[r]) {//左边小于右边 b[p++] = a[l++];//存左边 } else { b[p++] = a[r++];//存右边 } } while(l <= mid) b[p++] = a[l++];//特判左区间没有结束,直接全部拷贝到b数组 while(r <= right) b[p++] = a[r++];//特判右区间没有结束,直接全部拷贝到b数组 for(int i = left, p = 0; i <= right; i++,p++) { a[i] = b[p];//还给a数组(待排原数组) } }
九.算法复杂度的估算
1.多项式时间复杂度
- 定义:运行时间与输入数据规模$n$的某次幂成正比,常见形式包括:
- 线性复杂度 (单层循环)
- 平方复杂度 (双重嵌套循环)
- 立方复杂度 (三重嵌套循环)
- 示例:高精度乘法
2.指数时间复杂度
- 定义:运行时间随输入数据规模 呈指数级增长,常见形式如 。
- 示例:归并排序
3.对数时间复杂度
- 定义:运行时间与输入规模的对数相关,常见形式如 。
- 示例:二分查找每次将搜索范围减半
复杂度估算的对比案例
| 问题场景 | 低效方案(复杂度) | 高效方案(复杂度) |
|---|---|---|
| 在有序数组A中查找元素 | 遍历查找 | 二分查找 |
| 计算斐波那契数列 | 递归法 | 动态规划 |