质数筛法

要筛选出$2\sim{}n$以内的素数，一般有两种方法，一个是埃氏筛法，另一个是欧拉筛法。

埃氏筛与欧拉筛的实质:质数的倍数不是质数

埃氏筛法

埃拉托斯特尼筛法，简称埃氏筛，是一种由希腊数学家埃拉托斯特尼所提出的一种简单检定质数的算法。

要得到自然数 $n$ 以内的全部质数，把小于 $n$ 的所有质数的倍数剔除，剩下的就是质数。

• 从最小的质数2开始，逐步标记其倍数为非质数（合数）。
• 对于每个新发现的质数p，它会将p的倍数（从p^2开始，因为p之前的倍数已经被更小的质数标记过了）全部标记为非质数。
• 这种方法会多次标记同一个数（例如，30会被2、3和5都标记一次），导致一些不必要的计算。

例如 找30以内的质数，2、3、5、7、11、 13、 17、 19、23、29

（2）：4，6，8，10，12，14，16，18，20、22、24、26、28、30
（3）：9，12，15，18、21、24、27、30
 (4)：已经被2的倍数筛掉了
 (5)：10  20、30

时间复杂度 : O(nloglogn)

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
bool p[N];//标记数组
int main()
{
      int n;
      cin>>n;//范围2-n;
      memset(p,1,sizeof(p));//初始化都是质数 
      for(int i=2;i<=n/i;i++)
      {
          if(p[i])//筛掉i的倍数,i的倍数都不是质数 
          {
            //素数的倍数都是合数，为什么是j=j+i因为是倍数增加。注意改变的是j不是i。
              for(int j=i*2;j<=n;j=j+i)
              {
                  p[j]=0;//对合数进行标记。
            }
          }
      }
      for(int i=2;i<=n;i++)//遍历，没有标记的就说素数
      {
          if(p[i]==1){
              cout<<i<<" ";
        }
      }
      return 0;
}

从2开始，它是素数，所以内循环会标记4,6,8,10,12······一直到退出循环，然后当外层循环到3的时候，它又会标记6,9,12······，在这里我们就能看出一点问题，有数被重新标记了，而且循环到后面重复标记的数量一定不少。

有没有什么办法省掉无意义的步骤呢？

欧拉筛法（线性筛）

如果每个合数只被它的最小质因数筛除，那么每个数最多只被筛一次。

枚举2~n中的每一个数i:

• 如果i是质数则保存到质数表中
• 利用i和质数表中的质数prime[j]去筛除i*prime[j]，对于当前数i和已知质数prime[j]，如果i能被prime[j]整除，则停止用更大的质数去筛i的倍数，因为这样做将是重复的。
• 这种方法避免了重复筛选，提高了算法的效率。

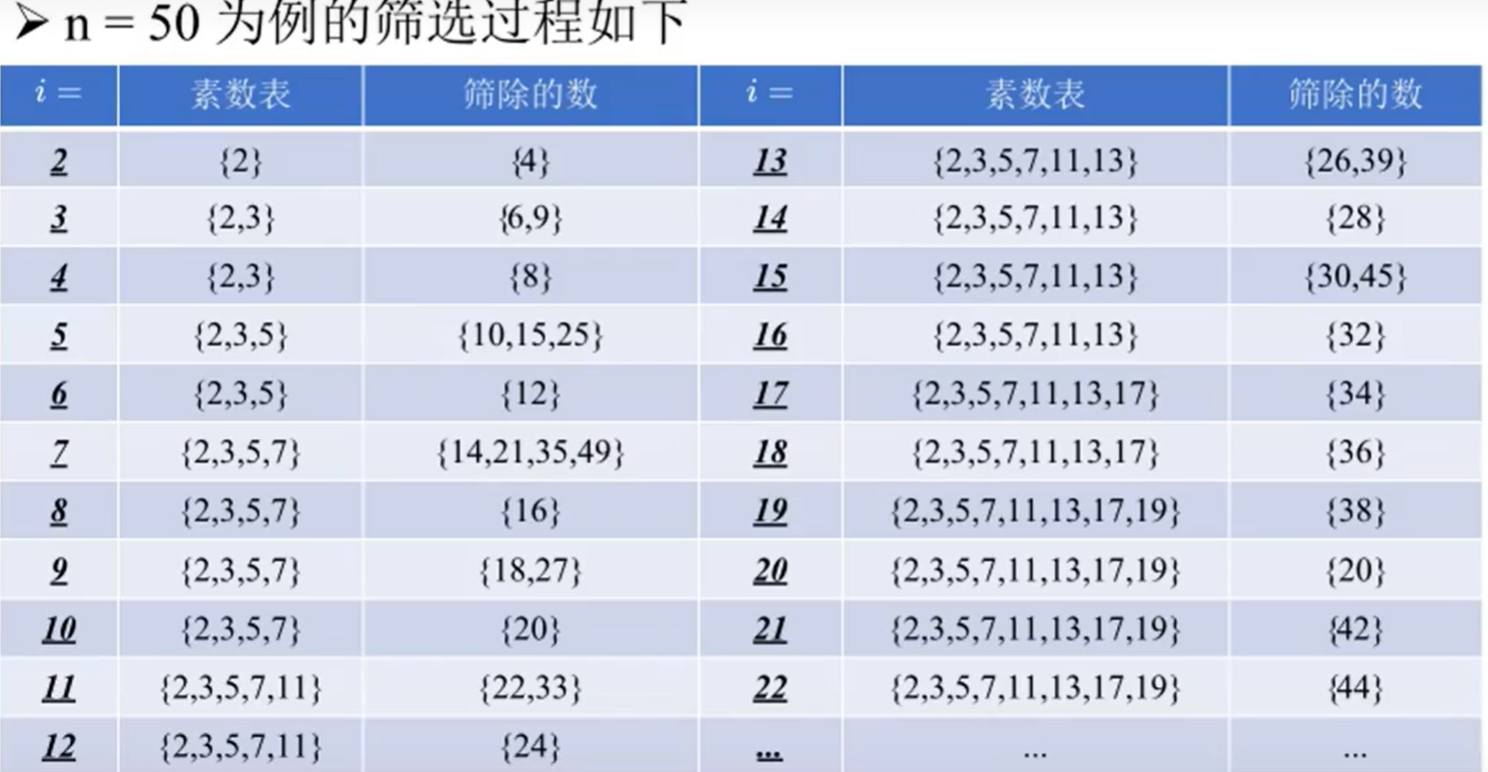
时间复杂度 : O(n)

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
bool b[N];//标记数组
int p[N],cnt; //存储质数的数组
int main() {
    int n;
    cin>>n;
    memset(b,1,sizeof(b));
    for(int i=2; i<=n; i++) {
        if(b[i]) p[++cnt]=i;//把质数保存到质数表中
        for(int j=1; j<=cnt&&i*p[j]<=n; j++) {
            b[i*p[j]]=0;//筛除 i*p[j]
            //判断是否能被最小质因数整除，确保每个数只被它的最小质因数筛除
            if(i%p[j]==0) break;
        }
    }
    for(int i=1;i<=cnt;i++){
        cout<<p[i]<<" ";
    }     
    return 0;
}

欧拉筛内部有一个很重要的判断语句：if(i%prime[j]==0)break; 就是这一个小步骤取消了多余的重复标记。

总结

欧拉筛法通过避免重复筛选，在埃氏筛法的基础上实现了时间复杂度的显著降低，是一种高效且实用的质数筛选算法。其核心思想在于确保每个合数只被其最小的质因子筛掉一次，从而提高了算法的效率。在实际应用中，欧拉筛法在处理大规模数据时表现出色，被广泛应用于密码学、数论、组合数学等领域。