一、树
1.什么是树?
如果有人问你什么是树?你可能首先想到的是大自然中的树木,它们有根、枝干和树叶,彼此之间有着明显的层次和联系。

数据结构中的 树 的名字由来,是因为如果把节点之间的关系直观展示出来,由于长得和现实世界中的树很像,由此得名
线性结构(数组、链表等)中节点是首位相接一对一关系,在树结构中节点之间不再是简单的一对一关系,而是较为复杂的一对多的关系
树在现实中是可以找到例子的,比如现实中的族谱,亲戚之间的关系是层次关联的树形关系
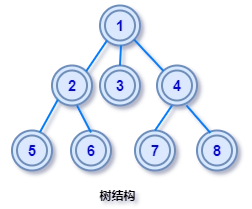
若 n 个结点由恰好 n-1 条边连接,且没有环,则这些结点和边构成的是一棵树。
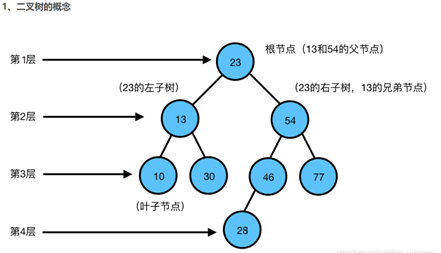
2.树的相关概念
树(Tree):有层次关系个节点的有限集合。
空树:N=0
非空树:有且仅有一个根节点
节点(Node)
树中的基本元素,包含数据和指向子节点的指针(或引用)。
边(Edge)
连接树中两个节点的连接线。
节点的度(Degree)
树中一个结点的子树个数,最大度数称为树的度。
根节点(Root)
树的顶层节点,没有父节点。
分支节点(Branch Node)
度大于0的节点
叶子节点(Leaf Node)
度为 0 的节点,直观来看叶子节点都位于树的最底层,就是没有分叉的节点
父节点(前驱) Parent Node
某个节点的上级节点
子节点(后继) Child Node
某个节点的下级节点。
兄弟节点(Brother Node)
具有相同父节点的节点
子树(Sub Tree)
除根外,可分为m个互不相交的有限集合。
节点的层次(Level)
从树的根开始,根结点为第一层,它的子结点为第二层,以此类推。
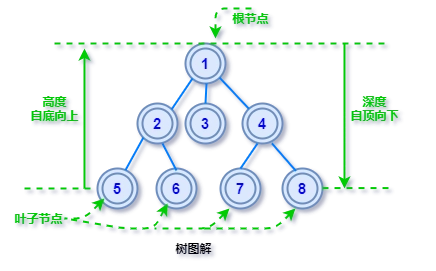
节点的高度(Height)
高度是从叶子节点开始「自底向上」逐层累加的路径长度,树叶的高度为 1
节点的深度(Depth)
深度是从根节点开始「自顶向下」逐层累加的路径长度,根的深度为1
二、树的种类
二叉树:每个节点最多含有两个子节点的树称为二叉树;
满二叉树:叶节点除外的所有节点均含有两个子树的树被称为满二叉树
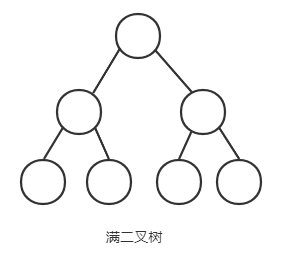
完全二叉树:二叉树除去最后一层为满二叉树,且最后一层的结点依次从左到右分布,这样的二叉树称为完全二叉树
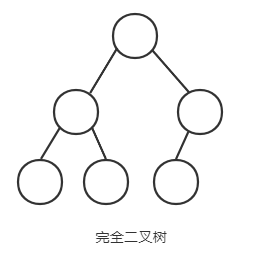
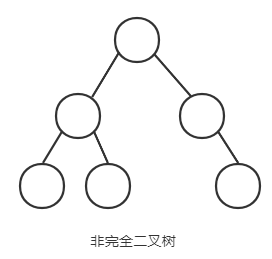
哈夫曼树:带权路径最短的二叉树称为哈夫曼树或最优二叉树
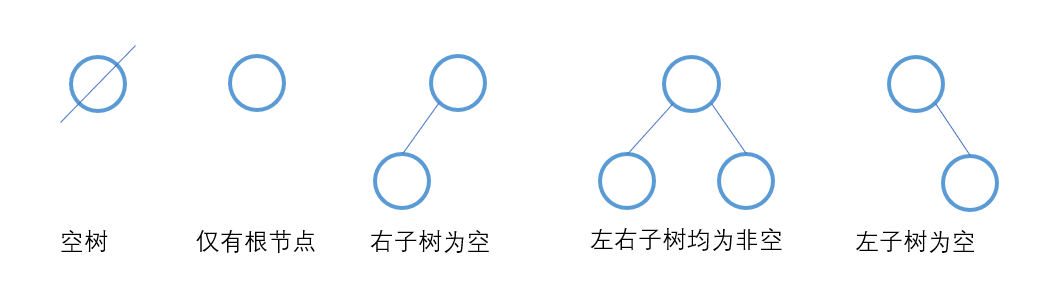
三、二叉树的基本形态
二叉树是n(n≥0)个结点的有限集合
四、二叉树的性质
性质1:在非空二叉树的第i层做多有$2^{i-1}$节点。
二叉树的每一层节点数最多按照指数级增长。
第一层(根节点所在层)有1个节点($2^0$=1 ) ,第二层最多有2个节点($2^1$=2 ),第三层最多有4个节点($2^2$=4 ),以此类推。每一层节点数是前一层节点数的两倍。
这个性质源于二叉树每个节点最多有两个子节点的特性。
性质2:深度为k的二叉树最多有$2^k -1$个节点。
深度为k的二叉树意味着它有k层。根据性质1,我们知道第i层最多有$2^{i-1}$个节点。将这一规律应用到每一层,累加所有层的节点数,得到的总节点数上限就是:$2^k -1$个节点
性质3:对于任意一棵二叉树,如果度为0的节点个数为n0。度为2的节点数为n2。则n0=n2+1
性质4:具有n个节点的完全二叉树的深度k=floor(log2n)+1
性质5:对于含n个节点的完全二叉树中编号为i(1<=i<=n)的节点。
- 如果i=1,则i节点是这可完全二叉树的根,没有双亲。否则其双亲编号为i/2
- 如果2i>n,则i节点没有左孩子,否则其左孩子的编号为2i
- 如果2i+1>n,则i节点没有右孩子,否则其右孩子的编号为2i+1
补充性质1:叶子结点数=度为2的结点+1
补充性质2:结点总数=n1+n2+n0 ( n1 是度为1的点,n2是度为2的点,n0是度为0点)
补充性质3:对于一棵完全二叉树来说,n1(度为1的点)只有1或0
补充性质4:结点总数=度数 * 该度数对应的结点数 + 1
五、二叉树的遍历
遍历表达法是有3种,先序遍历、中序遍历、后序遍历。
例如: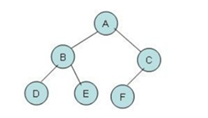
先序(根)遍历为ABDECF(根-左-右)
中序(根)遍历为DBEAFC(左-根-右)
后序(根)遍历为DEBFCA(左-右-根)
例2: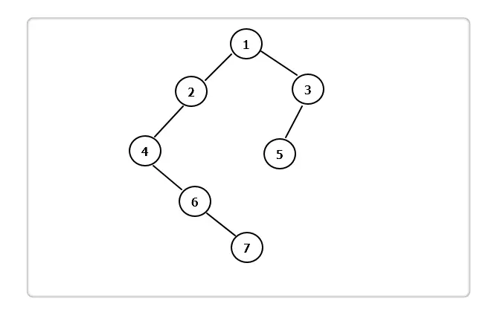
先序遍历:对于当前节点,先输出该节点,然后输出他的左孩子,最后输出他的右孩子。以上图为例,递归的过程如下: (1):输出 1,接着左孩子;
(2):输出 2,接着左孩子;
(3):输出 4,左孩子为空,再接着右孩子;
(4):输出 6,左孩子为空,再接着右孩子;
(5):输出 7,左右孩子都为空,此时 2 的左子树全部输出,2 的右子树为空,此时 1 的左子树全部输出,接着 1 的右子树; (6):输出 3,接着左孩子;
(7):输出 5,左右孩子为空,此时 3 的左子树全部输出,3 的右子树为空,至此 1 的右子树全部输出,结束。
结果:1246735
中序遍历:对于当前结点,先输出它的左孩子,然后输出该结点,最后输出它的右孩子。以上图为例: (1):1–>2–>4,4 的左孩子为空,输出 4,接着右孩子; (2):6 的左孩子为空,输出 6,接着右孩子; (3):7 的左孩子为空,输出 7,右孩子也为空,此时 2 的左子树全部输出,输出 2,2 的右孩子为空,此时 1 的左子树全部输出,输出 1,接着 1 的右孩子; (4):3–>5,5 左孩子为空,输出 5,右孩子也为空,此时 3 的左子树全部输出,而 3 的右孩子为空,至此 1 的右子树全部输出,结束。
结果:4672153
后序遍历:对于当前结点,先输出它的左孩子,然后输出它的右孩子,最后输出该结点。依旧以上图为例: (1):1->2->4->6->7,7 无左孩子,也无右孩子,输出 7,此时 6 无左孩子,而 6 的右子树也全部输出,输出 6,此时 4 无左子树,而 4 的右子树全部输出,输出 4,此时 2 的左子树全部输出,且 2 无右子树,输出 2,此时 1 的左子树全部输出,接着转向右子树; (2):3->5,5 无左孩子,也无右孩子,输出 5,此时 3 的左子树全部输出,且 3 无右孩子,输出 3,此时 1 的右子树全部输出,输出 1,结束。
结果:7642531
六、遍历与表达式
一棵二叉树的先序遍历的结果就是前缀表达式(波兰式)
一棵二叉树中序遍历的结果就是中缀表达式
一个二叉树后序遍历的结果就是后缀表达式(逆波兰式)
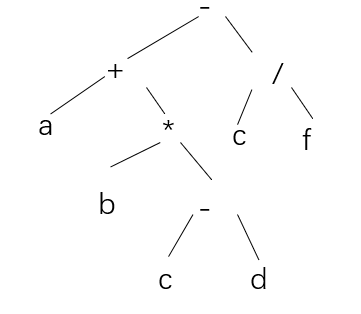
前缀表示: -+a*b-cd/ef
中缀表示: a+b*c-d-e/f
后缀表示: abcd-*+ef/-
结论:已知前序序列和中序序列可以确定二叉树
已知中序序列和后序序列也可以确定出二叉树
已知前序序列和后序序列不能确定二叉树
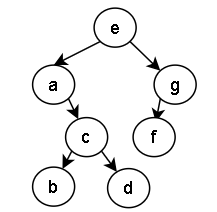
【例题】某二叉树的中序遍历为abcdefg,后序遍历为bdcafge,则先序遍历是_
【解析】记住一点:中序遍历确定左右子树,后(前)序遍历确定根结点。
(1)已知后序遍历为bdcafge(左右根),那么e一定是根结点;已知e是根结点,看中序遍历,那么abcd是左子树,fg是右子树
(2)先看左子树abcd,这几个符号在后序遍历中是bdca,所以a是根结点。那么再看中序遍历abcd,说明左子树为空,右子树是bcd。
(3) 继续看bcd,在后序遍历中出现的顺序是bdc,说明c是根结点,然后再看中序遍历,b是左子树,d是右子树。
(4) 看右子树fg,在后序遍历的顺序是fg,说明g是根结点。再看中序遍历fg。说明f是左子树,右子树为空。
 />
/>