简介

二叉树是最重要的基本数据结构，没有之一。

1、二叉树本身是比较简单的基础数据结构，但是很多复杂的数据结构都是基于二叉树的，比如 [红黑树]（二叉搜索树）、[多叉树]、[二叉堆]、[图]、[字典树]、[并查集]、[线段树]等等。你把二叉树玩明白了，这些数据结构都不是问题；如果你不把二叉树搞明白，这些高级数据结构你也很难驾驭。

2、二叉树不单纯是一种数据结构，更代表着递归的思维方式。一切递归算法，比如 [回溯算法]、[BFS 算法]、[动态规划]本质上也是把具体问题抽象成树结构，你只要抽象出来了，这些问题最终都回归二叉树的问题。同样看一段算法代码，在别人眼里是一串文本，每个字都认识，但连起来就不认识了；而在你眼里的代码就是一棵树，想咋改就咋改，咋改都能改对，实在是太简单了。

几种常见的二叉树

1、每个节点下方直接相连的节点称为子节点，上方直接相连的节点称为父节点。比方说节点 3 的父节点是 1，左子节点是 5，右子节点是 6；节点 5 的父节点是 3，左子节点是 7，没有右子节点。

2、我们称最上方那个没有父节点的节点 1 为根节点，称最下层没有子节点的节点 4、7、8 为叶子节点。

3、我们称从根节点到最下方叶子节点经过的节点个数为二叉树的最大深度/高度，上面这棵树的最大深度是 4，即从根节点 1 到叶子节点 7 或 8 的路径上的节点个数。

满二叉树

满二叉树就是每一层节点都是满的，整棵树像一个正三角形：

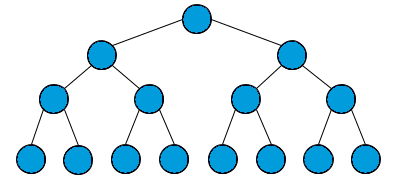
满二叉树有个优势，就是它的节点个数很好算。假设深度为 h，那么总节点数就是 2^h - 1，等比数列求和。

完全二叉树

完全二叉树是指，二叉树的每一层的节点都紧凑靠左排列，且除了最后一层，其他每层都必须是满的：

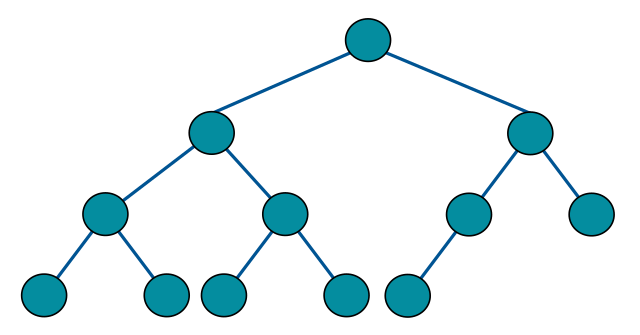
不难发现，满二叉树其实是一种特殊的完全二叉树。

完全二叉树的特点：由于它的节点紧凑排列，如果从左到右从上到下对它的每个节点编号，那么父子节点的索引存在明显的规律。

平衡二叉树

平衡二叉树（Balanced Binary Tree）是一种特殊的二叉树，它的「每个节点」的左右子树的高度差不超过 1。

要注意是每个节点，而不仅仅是根节点。

比如下面这棵二叉树树，根节点 1 的左子树高度是 2，右子树高度是 3；节点 2 的左子树高度是 1，右子树高度是 0；节点 3 的左子树高度是 2，右子树高度是 1，以此类推，每个节点的左右子树高度差都不超过 1，所以这是一棵平衡二叉树：

下面这棵树就不是平衡二叉树，因为节点 2 的左子树高度是 2，右子树高度是 0，高度差超过 1，不符合条件：

假设平衡二叉树中共有 NN 个节点，那么平衡二叉树的高度是 O(log⁡N)。这是非常重要的性质，后面讲到的红黑树和线段树会利用平衡二叉树的这个性质，保证算法的高效性。

二叉搜索树

二叉搜索树（Binary Search Tree，简称 BST）是一种很常见的二叉树，它的定义是：

对于树中的每个节点，其左子树的每个节点的值都要小于这个节点的值，右子树的每个节点的值都要大于这个节点的值。你可以简单记为「左小右大」。

不要只看子节点，而要看整棵子树的所有节点。

比方说，下面这棵树就是一棵 BST：

节点 7 的左子树所有节点的值都小于 7，右子树所有节点的值都大于 7；节点 4 的左子树所有节点的值都小于 4，右子树所有节点的值都大于 4，以此类推。

相反的，下面这棵树就不是 BST：

如果你只注意每个节点的左右子节点，似乎看不出问题。你应该看整棵子树，注意看节点 7 的左子树中有个节点 8，比 7 大，这就不符合 BST 的定义了。

BST 是非常常用的数据结构。因为左小右大的特性，可以让我们在 BST 中快速找到某个节点，或者找到某个范围内的所有节点，这是 BST 的优势所在。

比方说，对于一棵普通的二叉树，其中的节点大小没有任何规律可言，那么你要找到某个值为 x 的节点，只能从根节点开始遍历整棵树。

而对于 BST，你可以先对比根节点和 x 的大小关系，如果 x 比根节点大，那么根节点的整棵左子树就可以直接排除了，直接从右子树开始找，这样就可以快速定位到值为 x 的那个节点。

二叉树的实现方式

最常见的二叉树就是类似链表那样的链式存储结构，每个二叉树节点有指向左右子节点的指针，这种方式比较简单直观。

class TreeNode {
public:
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

// 你可以这样构建一棵二叉树：
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->right->left = new TreeNode(5);
root->right->right = new TreeNode(6);

// 构建出来的二叉树是这样的：
//     1
//    / \
//   2   3
//  /   / \
// 4   5   6

在一般的算法题中，我们可能会把实际问题抽象成二叉树结构，但我们并不需要真的用 TreeNode 创建一棵二叉树出来，而是直接用类似哈希表的结构来表示二叉树/多叉树。

// 1 -> {2, 3}
// 2 -> {4}
// 3 -> {5, 6}

unordered_map<int, vector<int>> tree;
tree[1] = {2, 3};
tree[2] = {4};
tree[3] = {5, 6};

05-二叉树

简介