什么是贪心算法？

算法思想：

遵循某种规律，不断选取当前最优策略的算法设计方法（不从整体考虑，仅“目光短浅”的考虑当前的局部最优解）。贪心没有固定的算法框架，算法设计的关键是贪心策略的选择。

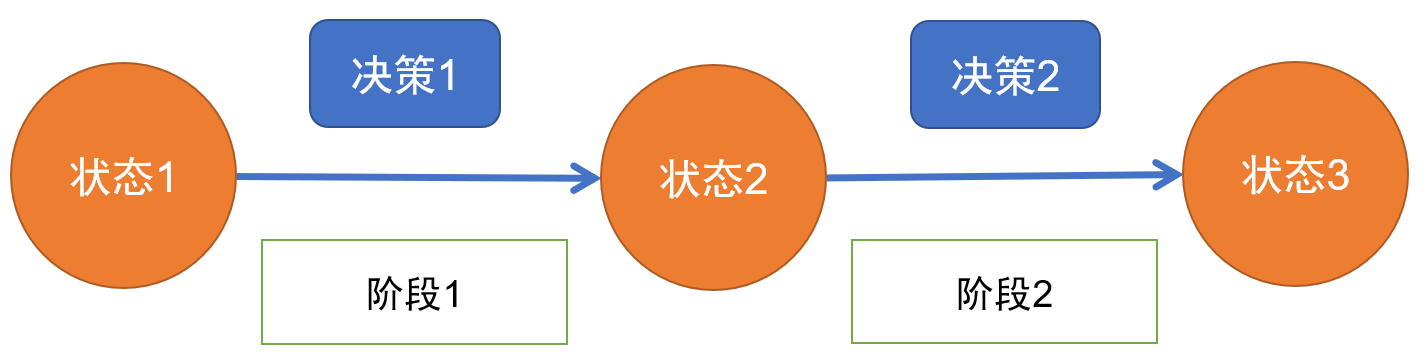
多阶段决策过程: 问题可以按时间顺序分解成若干相互联系的阶段，在每一个阶段都要做出决策，全部过程的决策是一个策略。

最优子结构和无后效性

最优子结构指的是，问题的最优解包含子问题的最优解。

反过来说：我们可以通过求解子问题的最优解，推导出问题的最优解。

无后效性，有两层含义：

• 在推导后面阶段状态的时候，我们只关心当前阶段的状态值，不关心这个状态是怎么一步步推导出来的。
• 某阶段状态一旦确定，就不受之后阶段的决策影响。

贪心问题解题过程

1. 建立数学模型

2. 确定最优子结构

   如何将要求解的大问题分解成子问题

3. 思考贪心策略选择的条件

   应该选择满足什么条件的元素加入解

4. 证明贪心选择性质

活动安排问题解题过程

1. 建立数学模型

2. 确定最优子结构

   选择一个活动后，在n-1个活动中选择最多的不重叠的活动

3. 思考贪心策略选择的条件

   选择：不与已选择活动重叠的，结束时间最早的活动

4. 证明贪心选择性质

证明贪心选择性质

要想证明贪心选择能否得到最优解，只需要证明最优解包含每一次的贪心选择。

使用数学归纳法：

• 是否存在最优解包含第一次的贪心选择
• 假设存在最优解包含前k次的贪心选择，该最优解是否包含第k+1次的贪心选择

证明：存在最优解包含第一次的贪心选择

使用反证法

• 假设所有最优解都不包含第一次的贪心选择
• 对于某一最优解，如果第一次采用贪心选择，也仍然能得到最优解。这与假设相悖。
• 原命题得证。

证明：在k次贪心选择后，存在最优的活动选择方案包含第k+1次的贪心选择：不与前面重叠的结束时间最早的活动$A_g$。

• 假设所有最优解都不包含活动$A_g$
• 对于某一最优解，活动序列按结束时间排序为：$A_1,A_2,...,A_k,A_{k+1},...,A_n$，如果将$A_g$替换$A_{k+1}$，仍然能形成最优解，这与假设相悖。
• 原命题得证。