什么是递推算法？

递推算法，是指从已知的初始条件出发，依据某种递推关系，逐次推出所要求的各中间结果及最后结果。

递推则是由“边界”往“结果”一步步求解。

#include <iostream>
using namespace std;
int a[50],n,num;
int main() {
    cin>>n;
    a[1]=1;
    a[2]=1;
    for(int i=3; i<=n; i++) {
        a[i]=a[i-1]+a[i-2];
    }
    cout<<a[n]<<endl;
    return 0;
}

递推需要想清楚求解顺序比如求 a[i] 时需要用到 a[i-1] 和 a[i-2]，那么就需要先算完这两项后才能算 a[i]。必须按照从小到大的顺序枚举。

特点：

1.问题可以划分成多个状态；

2.除初始状态外，其它各个状态都可以用固定的递推关系式来表示。

首要问题：得到相邻的数据项间的关系（即递推关系）。

一般来说，可以将递推算法看成是一种特殊的迭代算法。

递推与迭代比较，两者的时间复杂度是相同的。所不同的是，递推往往设置数组，而迭代只要设置迭代的简单变量即可。

递推过程中数组变量带有下标，推出过程比迭代更为清晰。也正因为递推中应用数组，因此保留了递推过程中的中间数据。

递推关系式

给定一个数的序列 $F_0,F_1,...,F_n$，若存在整数 $n_0$，使当 $n>n_0$时，可以用符号（或大于号、小于号）将$F_n$ 与其前面的某些项$F_i(0<i<n)$ 联系起来，这样的式子就叫做递推关系式。例如：$F_n=F_{n-1}+F_{n-2}$

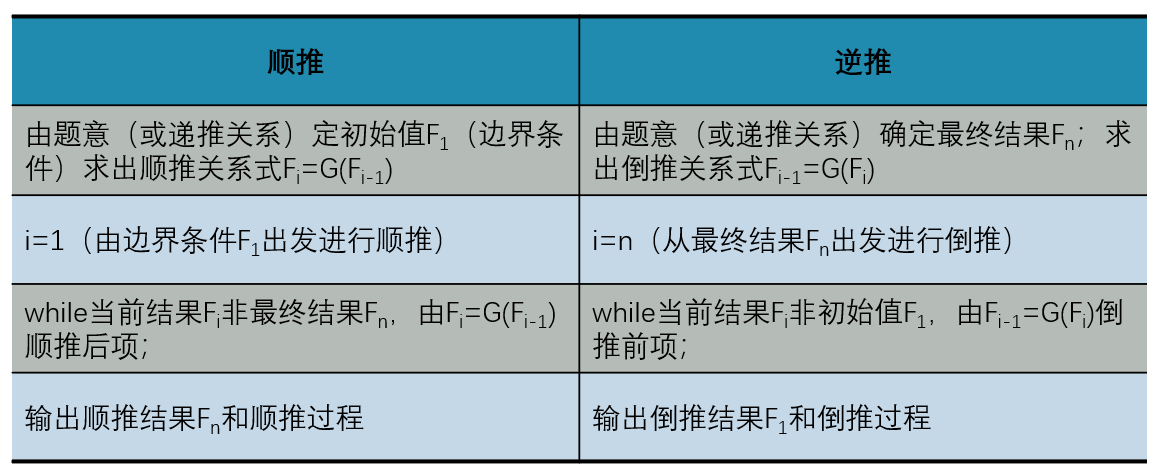
解决递推问题的一般步骤：

1.建立递推关系式（顺推或逆推）；

2.确定边界条件（即初始值）；

3.递推求解。

训练题单

作业