思考

分香蕉

6 根香蕉，恰好平分给 N 位同学（每位同学分到的香蕉完整且数量相同），请问 N 能取哪些 值？

解题思路：分别以 1 到 6 假设 N，发现只有 N=1，2，3，6 这 4 个数字满足这道题目。

在这道简单的题目里面，已经用到了整除的概念，可以看出来，整数之间的整除性，体现为 两整数相除没有余数。

整除的定义（倍数和约数）

设 a,b 是两个整数，且 a≠0, 如果存在一个整数 c，使得 b=c×a, 那么就说 b 可以被 a 整除, 且称 b 是 a 的倍数，a 是 b 的约数(也称作因数)**。

6 = 2 × 3，6 是 3 的倍数，3 是 6 的约数(因数) 。

例如：

60 ÷ 6 = 10，这里 10 和 6 是 60 的约数，60 是 10 和 6 的倍数。

10 ÷ 2 = 5， 这里 2 和 5 是 10 的约数，10 是 2 和 5 的倍数。

15 ÷ 5 = 3， 这里 3 和 5 是 15 的约数，15 是 3 和 5 的倍数。

总结：

如果 a × b = c（a、b、c 都是不为 0 的整数）,那么 a 是 c 的约数，b 也是 c 的约数；c 是 a 的倍数，c 也是 b 的倍数。

约数和倍数是互相依存的。

质数

一个数除了 1 和它本身，不再有别的约数，这个数就叫做质数。它是一个独立存在的数。

比如 17 是质数，因为它只有 1 和 17 两个约数。质数只有两个约数。

合数

一个数除了 1 和它本身，还有别的约数，这个数就叫做合数。

比如 12 是质数，因为除了 1 和 12 两个约数之外，还有 2，3，4，6 这些约数。合数最少有 3 个约数。

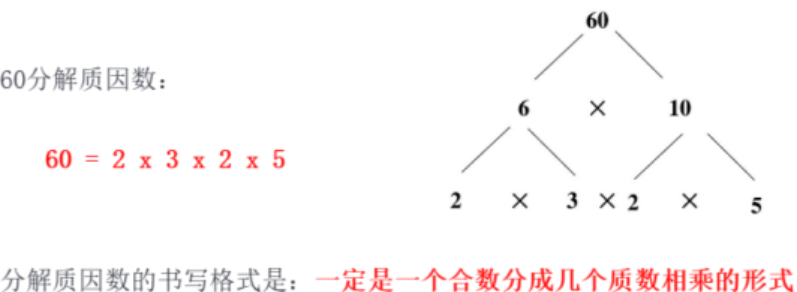
分解质因数

每个合数都可以写成几个质数相乘的形式，其中每个质数都是这个合数的因数（约数），叫 做这个合数的质因数。

质因数既是质数，也是因数。

把一个合数用质因数相乘的形式表示出来，叫做分解质因数。

最大公约数

思考

有两根长度分别为 20cm 和 30cm 的木棍，现在需要将它们分割成相同的长度，每根不能有剩 余，请问最大的长度是多少？

解题思路：可以使用列举法，分割为 1、2、5、10cm 时都不会有剩余，最大是 10cm。即最大 公约数。

最大公约数的定义

最大公约数（greatest common divisor，简写为 gcd）。

设 a1 和 a2 是两个整数，如果 a1 能被 d 整除，a2 也能被 d 整除，那么 d 就被称为 a1 和 a2 的公约数。其中最大的称为 a1 和 a2 的最大公约数。

例如：

求 12 和 18 的最大公约数？

12 = 2 × 2 × 3 18 = 2 × 3 × 3

质因数 2,3 是 12 和 18 这两个数共有的，所以 2x3（质因数的乘积）就是 12 和 18 的最大公 约数。

求 9 和 18 的最大公约数？

9 = 3 × 3 18 = 2 × 3 × 3

总结：

求几个数的最大公约数，先把这些数分解质因数，再将质因数的公共部分相乘即可。

最小公倍数

思考

有一个长木棍，既可以恰好切出若干根 10cm 的木棍，又可以切出若干根 20cm 的木棍，请问 这根长木棍最短的长度可以是多长？

解题思路：想恰好切出若 10cm，同时还可以切出若干 20cm，最短的长度为 30cm。即最小公 约数。

最小公倍数的定义

设 a1 和 a2 是两个整数，如果 d 能被 a1 整除，d 也能被 a2 整除，那么 d 就被称为 a1 和 a2 的公倍数。其中最小的称为 a1 和 a2 的最小公倍数。

例如：

10 = 2 × 5

25 = 5 × 5

最小公倍数： 2 × 5 × 5

求最小公倍数（分解质因数法）

最小公倍数等于它们所有的质因数的乘积（如果有几个质因数相同，则乘于两个数当中拥有 更多的质因数的次数）

例如：

求 18 和 27 的最小公倍数？

18 = 2 × 3 × 3 27 = 3 × 3 × 3

最小公倍数 = 2 × 3 × 3 × 3 = 54