前缀和
前缀和指数组或序列中每个位置之前的元素总和,可以把它理解为数学上的数列的前n项和,是一种重要的预处理方式,能大大降低查询的时间复杂度。
一维前缀和
原数组:a[1] ,a[2],a[3]…..a[n]
sum[0]=a[0];
sum[1]=a[0]+a[1];
sum[2]=a[0]+a[1]+a[2];
sum[3]=a[0]+a[1]+a[2]+a[3]
sum[4]=a[0]+a[1]+a[2]+a[3]
sum[5]=a[0]+a[1]+a[2]+a[3]+a[4]
前缀和:sum[i]=a[1]+a[2]…..a[i]
求前缀和公式:sum[i]=sum[i-1]+a[i] ,sum[0]=0;
| 序号i | 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|---|
| 原数组 | a[6] | 0 | 3 | 5 | 8 | 2 | 7 |
| 前缀和 | sum[6] | 0 | 3 | 8 | 16 | 18 | 25 |
作用:频繁求区间的和,原数组[l,r]的和sum
使用原数组计算,则需要从下标l到下标r遍历原数组求和:
sum=a[l]+a[l+1]…..+a[r];
使用前缀和计算:sum=sum[r]-sum[l-1]
一维前缀和案例
描述
输入n个整数,再输入m个区间,每个区间的起点下标L,终点下标R。对于每个区间,输出n个整数中从下标L到下标R的区间和
输入描述
第一行包括两个整数n和m。(1≤n,m≤100000)
第二行包括n个整数。(1≤整数≤100)接下来有m行,每行包含两个整数L和R,表示区间范围。(0<L≤R≤n)
输出描述
输出有m行,每行一个整数,表示一个区间和。
样例输入
10 3
2 1 3 6 4 20 15 10 4 11
3 7
1 9
5 8
样例输出
48
65
49
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,m,l,r,a[N],sum[N];//sum[i]表示的状态就是从1到i的区间和
int main()
{
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
sum[i]=a[i]+sum[i-1];
}
cin>>m;
for(int i=1;i<=m;i++){
cin>>l>>r;
cout<<sum[r]-sum[l-1]<<endl;
}
return 0;
}
二维前缀和
在一维前缀和的基础上,现在所求的是矩阵内一个任意的子矩阵的数的和,这样的问题我们就可以用二维前缀和进行求解。
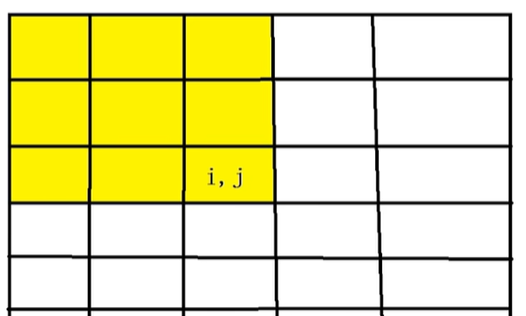
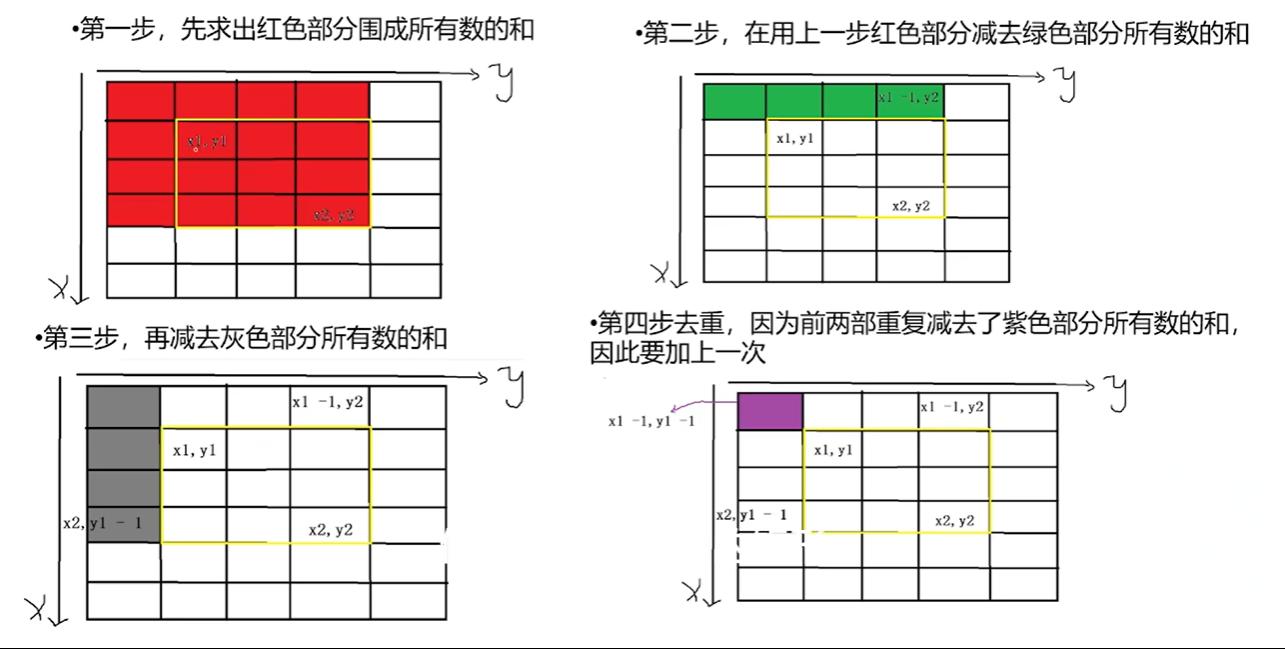
1.先求出红色部分所有数的和
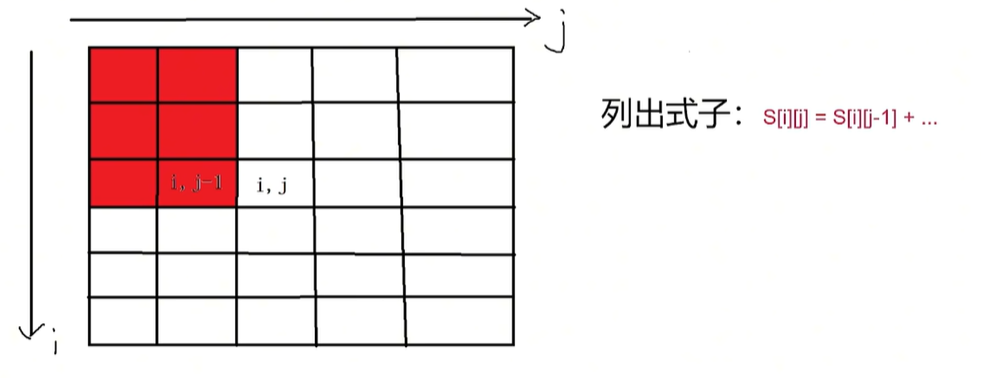
2.再求出绿色部分所有数的和
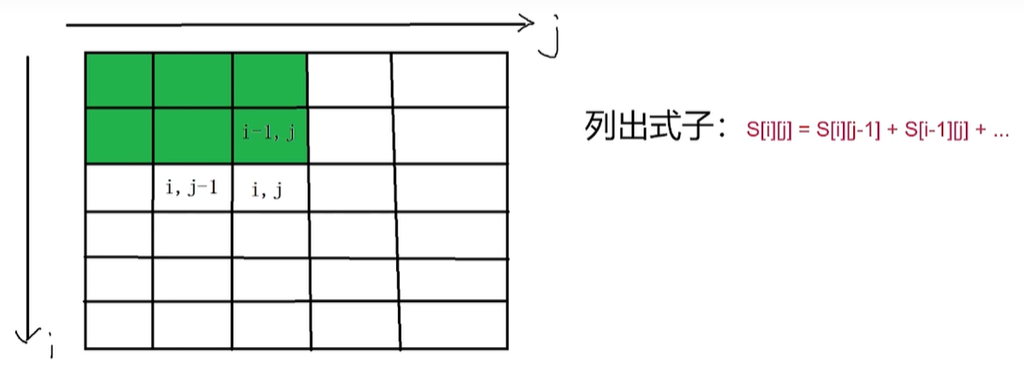
3.去重,因为前两步重复加上了黑色部分所有数的和,因此要减掉一次。
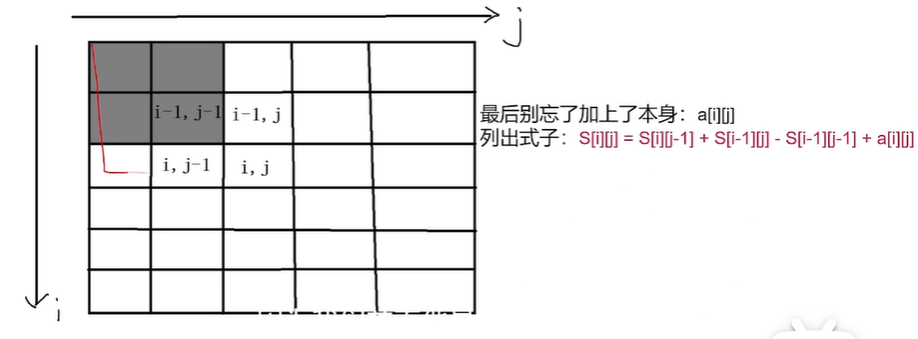
子矩阵的计算
处理二维前缀和
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j];
查询二维前缀和
int x1,y1,x2,y2;//待查询的点A(x1,y1)左上角 B(x2,y2)右下角
int ans=sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y1-1];//ans:答案
差分
一维差分
差分数组存储原数组的相邻两数之差。
原数组: a[1],a[2]…..a[n]
d[0]=a[0]
d[1]=a[1]-a[0]
d[2]=a[2]-a[1]
d[3]=a[3]-a[2]
d[4]=a[4]-a[3]
差分数组:d[1],d[2]…..d[n]
d[n]=a[n]-a[n-1]
求前缀和公式:sum[i]=sum[i-1]+d[i] ;
| 序号 | i | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|---|
| 原数组 | a[6] | 0 | 3 | 5 | 8 | 2 | 7 |
| 差分数组 | d[6] | 0 | 3 | 2 | 3 | -6 | 5 |
作用: 频繁修改区间,求原数组[L,R]的数全部加上c ,即a[L]+c,a[L+1]+c, a[R]+c,可以通过操作差分数组进行计算: 即,d[L]+c,d[R+1]-c
(1)原数组a在[1,3]区间加10,得到新数组c:
| 序号 | i | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|---|
| 原数组 | a[6] | 0 | 3 | 5 | 8 | 2 | 7 |
| 新数组 | c[6] | 0 | 13 | 15 | 18 | 2 | 7 |
(2)c[6]对应差分数组d c[i]=d[i]+c[i-1]
| 序号 | i | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|---|
| 新数组 | c[6] | 0 | 13 | 15 | 18 | 2 | 7 |
| 差分数组 | d[6] | 0 | 13 | 2 | 3 | -16 | 5 |
(3)a在[1,3]区间加10,对应的差分数组d的变化:d[1]+10,d[4]-10
解题过程:
(1)初始化原数组a
(2)求原数组a的差分数组d
(3)求原数组[L,R]的数全部加上c,可以直接操作差分数组d:d[L]+c,d[R+1]-c
(4)根据差分数组d ,求对应的前缀和数组。
一维差分案例
描述
在一个桌子上摆放了 n 个杯子,每个杯子中有一定量的水。小 A 同学负责向杯子中倒水,他总共倒了 k 次,每次会向从第 L 个杯子到第 R 个杯子中添加 P 毫升的水(注意:水只可能增加,不可能减少)。请问小 A 同学倒了 k 次水之后, n 个杯子每个杯子有多少毫升的水。
输入描述
第一行包含两个整数 n 和 k。
第二行包含 n 个整数,表示一开始每个杯子中水的毫升数。
接下来 k 行,每行包含三个整数 L,R,P表示一次操作。
输出描述
共一行,包含 n 个整数,表示最终 n 个杯子每个杯子有多少毫升的水。
样例输入
8 3
1 2 10 8 1 5 1 1
7 8 12
1 8 4
2 3 12
样例输出
5 18 26 12 5 9 17 17
代码实现
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,k,l,r,p,a[N],dif[N];
int main()
{
cin>>n>>k;
for(int i=1;i<=n;i++){
cin>>a[i];//原数组
dif[i]=a[i]-a[i-1];//原数组的差分数组
}
for(int i=1;i<=k;i++){
cin>>l>>r>>p;
dif[l]+=p;//操作差分数组
dif[r+1]-=p;
}
//计算前缀和
for(int i=1;i<=n;i++){
a[i]=dif[i]+a[i-1];
cout<<a[i]<<" ";
}
return 0;
}
总结
- 差分算法可以快速修改序列中某一段连续区间的值。过程如下:
- 在原序列的基础上构造差分数组
- 给区间[L , R] 的元素加上k,那么只需要将差分数组d [ L ] + = k ,d [ R + 1 ] − = k
- 对差分数组计算前缀和来还原出更新之后的序列。
二维差分
二维差分数组是二维前缀和数组的逆运算。
当我们想要对原始二维数组
a[n][m]的某个子矩阵区域进行频繁的加减操作时,可以借助一个辅助的差分数组d[n][m],将对整个区域的更新操作转化为对差分数组的四个顶点的操作,从而将每次更新的时间复杂度从 O(n*m) 降为 O(1)。最后,通过对差分数组进行一次二维前缀和计算,即可得到更新后的原始数组。
核心思想
二维差分的核心思想是:将对一个子矩阵的加减操作,转化为对差分矩阵四个角的常数操作。
假设我们有一个原始矩阵 a,我们想构建它的差分矩阵 d。它们的关系如下:
1. 定义差分数组 d
d[i][j] 的值,可以通过原始矩阵 a 来定义:
d[i][j] = a[i][j] - a[i-1][j] - a[i][j-1] + a[i-1][j-1]
2. 最关键的部分:进行区域更新?

左上加,右上减,左下减,右下加
//计算影响的4个格子
d[a1][b1]+=c; //左上角起点 (a₁, b₁)
d[a2+1][b2+1]+=c;//右下角外侧 (a₂+1, b₂+1)
d[a2+1][b1]-=c; //左下角外侧 (a₂+1, b₁)
d[a1][b2+1]-=c; //右上角外侧 (a₁, b₂+1)
完成所有更新操作后,对差分数组 d 求一次二维前缀和,得到的矩阵 a 就是最终答案。
代码模板
#include<bits/stdc++.h>
using namespace std;
int n,m,q,a1,b1,a2,b2,c,a[1005][1005],d[1005][1005];
int main(){
cin>>n>>m>>q;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
d[i][j]=a[i][j]-a[i][j-1]-a[i-1][j]+a[i-1][j-1];//差分数组
}
}
while(q--){
cin>>a1>>b1>>a2>>b2>>c;
//计算影响的4个格子
d[a1][b1]+=c;
d[a2+1][b2+1]+=c;
d[a2+1][b1]-=c;
d[a1][b2+1]-=c;
}
//前缀和,还原数组
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
a[i][j]=a[i-1][j]+a[i][j-1]-a[i-1][j-1]+d[i][j];
cout<<a[i][j]<<" ";
}cout<<endl;
}
return 0;
}
应用场景对比
前缀和适合:
- 频繁查询区间和
- 数据不经常变化
- 需要快速的区间查询
差分适合:
- 频繁进行区间增减操作
- 数据经常变化
- 最终只需要得到修改后的结果
选择建议
如果查询操作远多于修改操作,选择前缀和 如果修改操作远多于查询操作,选择差分 �