二分查找
二分查找，也称折半搜索，是用来在一个有序数组中查找某一元素的算法。
二分思想
- 二分查找要求搜索的区间是有序的；
- 二分查找是通过不断缩小解可能存在的范围，从而求得问题最优解的方法;
- 二分查找每一次检查范围的中点，从而确定答案的位置在中点的左边还是右边，这样每次就能把问题的可能存在范围缩小一半；
查找思路
对于有序数列（从小到大），设定左端 L（最小元素下标）和右端 R（最大元素下标）
当满足条件 L<=R 时，求中点 mid，将中点元素的值与所要查找的值比较。
如果中间元素刚好是要找的，就结束搜索过程；
如果中点元素值比所要查找元素大，那么右侧的只会更大，则应找前半段，所以 R=mid-1。
- 否则应找后半段 L = mid + 1，直到找到为止。
- 若 L > R，则说明找不到。
代码模板
1.最基本的二分查找算法
int ans=-1;//保存答案
while(l<=r){
int mid=(l+r)/2;
if(a[mid]==x){
ans=mid;//更新答案
break;
}else if(a[mid]>x){//前半段
r=mid-1;
}else if(a[mid]<x){//后半段
l=mid+1;
}
}
2. 寻找左侧边界的二分查找
例如 1 2 3 3 3 4 4 5 8 10
int ans=-1;//保存答案
while(l<=r){
int mid=(l+r)/2;
if(a[mid]==x){
ans=mid;//更新答案
r=mid-1;//继续向左查找
}else if(a[mid]>x){//前半段
r=mid-1;
}else if(a[mid]<x){//后半段
l=mid+1;
}
}
3.寻找右侧边界的二分查找
例如 1 2 3 3 3 4 4 5 8 10
int ans=-1;//保存答案
while(l<=r){
int mid=(l+r)/2;
if(a[mid]==x){
ans=mid;//更新答案
l=mid+1;//继续向右查找
}else if(a[mid]>x){//前半段
r=mid-1;// 搜索区间变为 [l, mid-1]
}else if(a[mid]<x){//后半段
l=mid+1;//搜索区间变为 [mid+1, r]
}
}
例题：升序数组，各元素不同，查找某元素。
如果该元素存在：输出该元素的下标；
如果不存在该元素，输出 -1。
在数字序列中 1 3 4 6 7 9 11 16 23 45，查找 11 的位置：
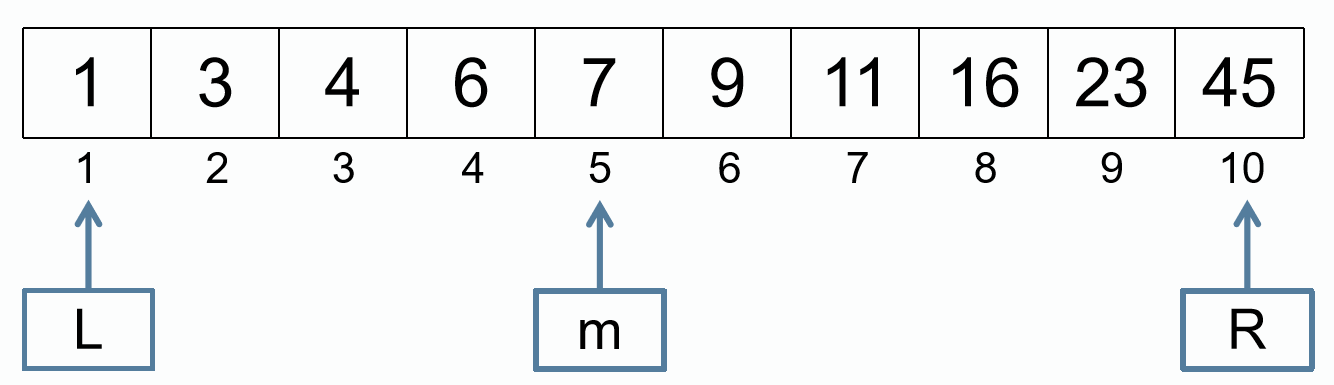
m = (L + R) / 2
L = m + 1
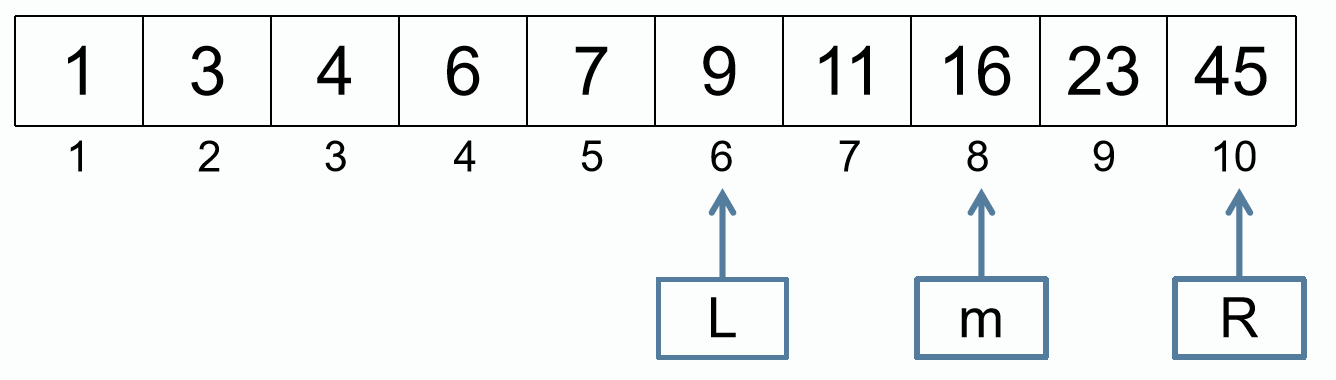
m = (L + R) / 2
R = m - 1
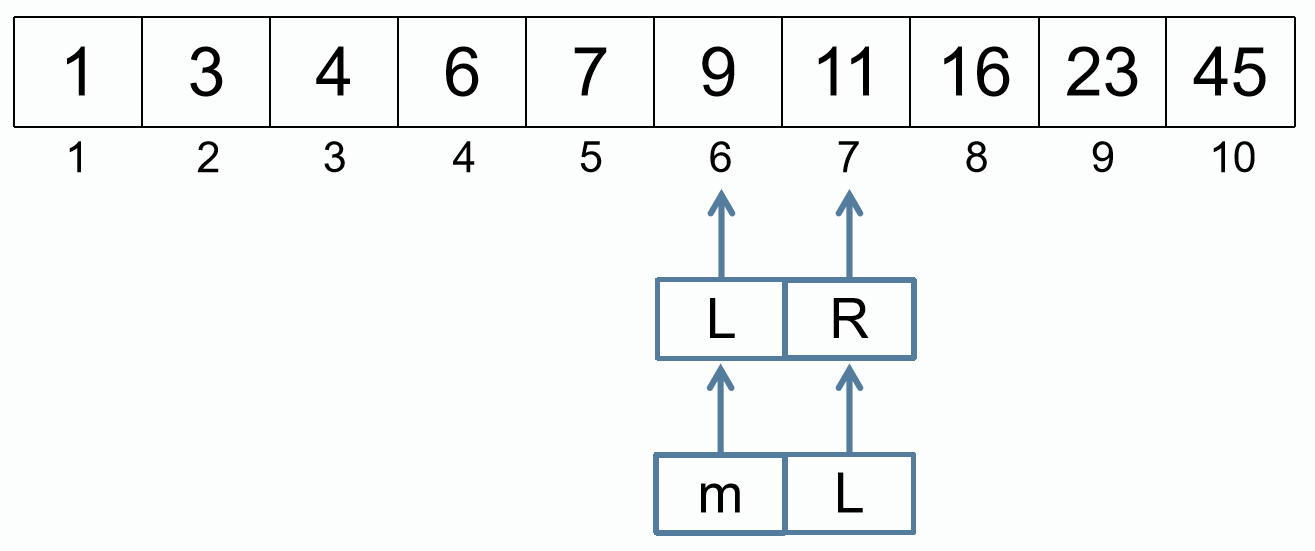
m = (L + R) / 2
L = m + 1
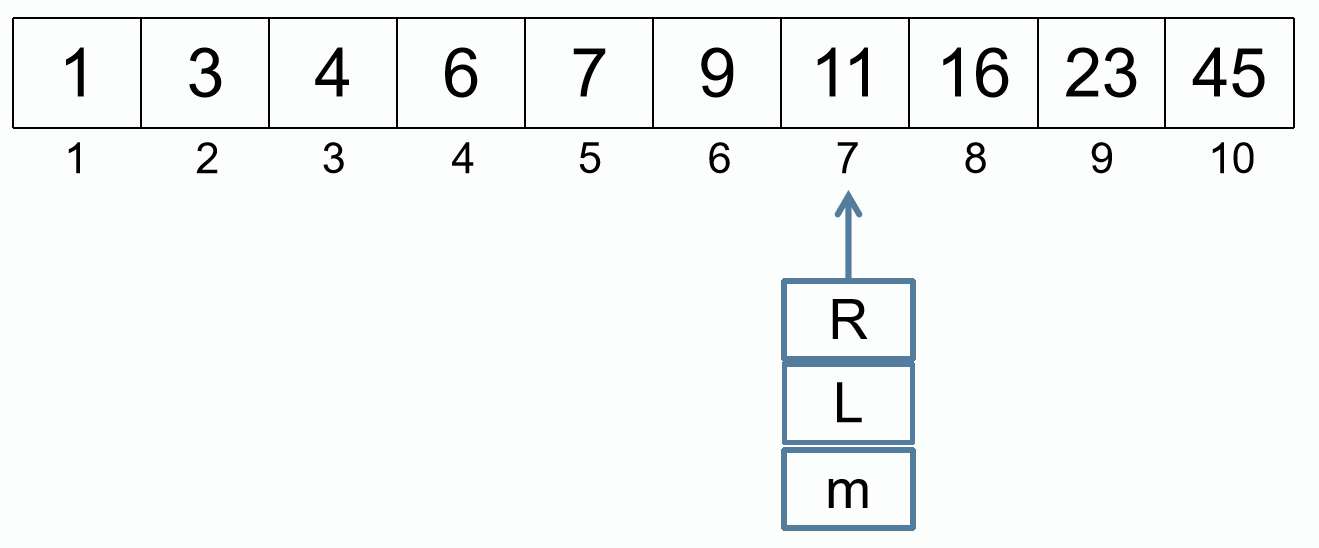
m = (L + R) / 2
找到 11 的位置是 7。
查找 10 的位置
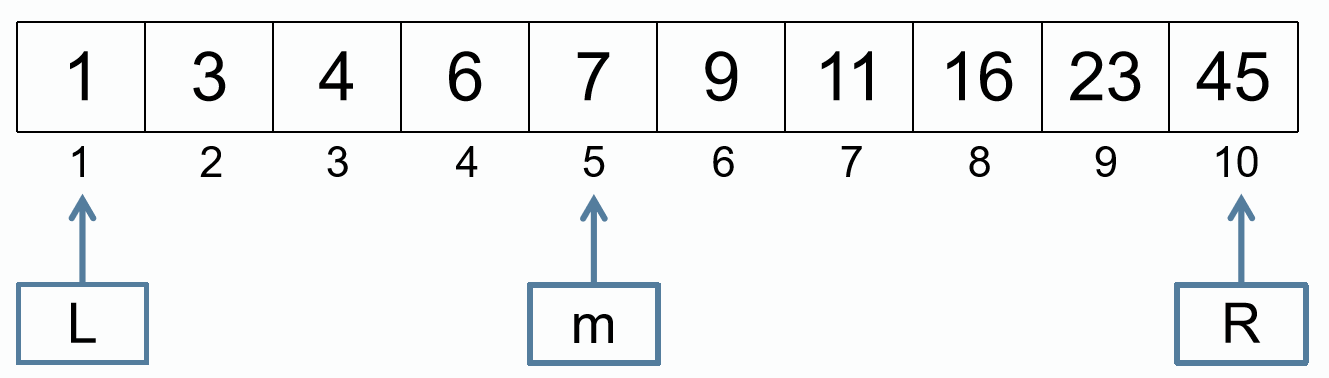
m = (L + R) / 2
R = m - 1
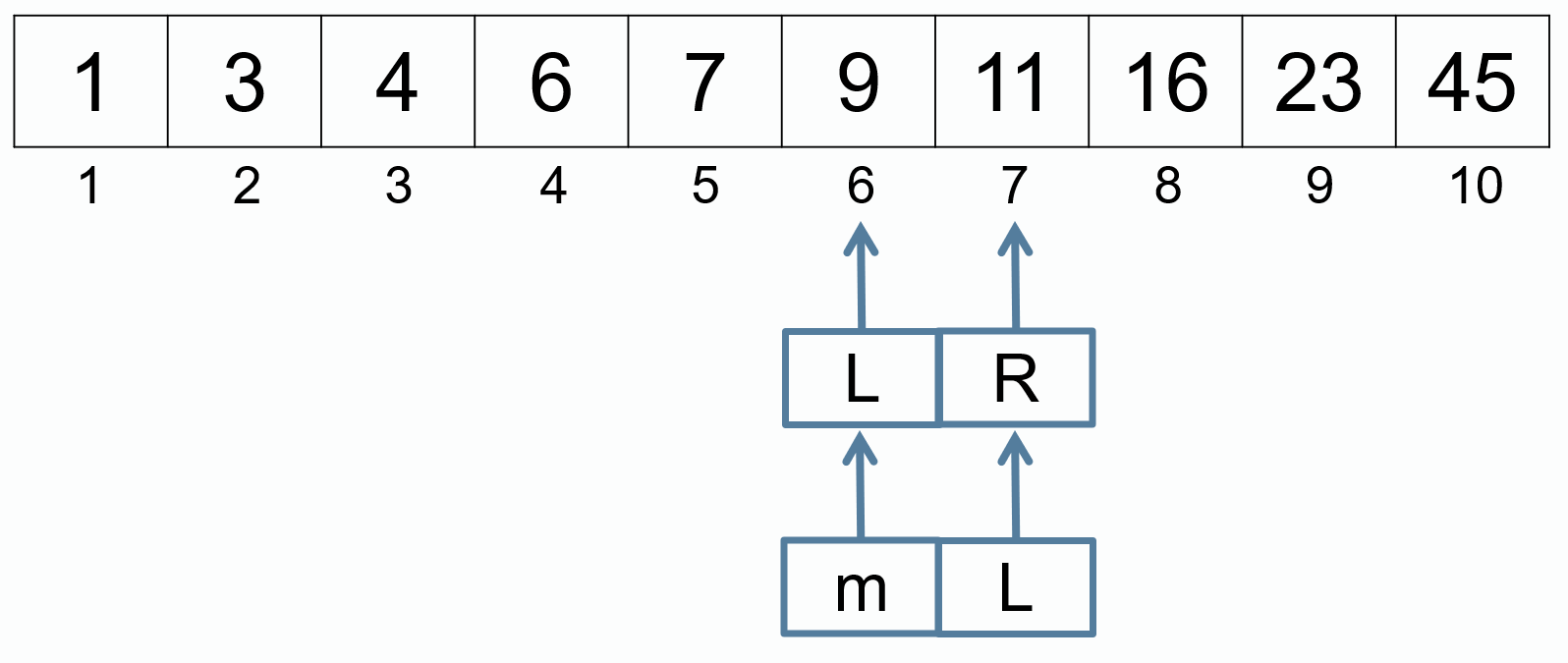
m = (L + R) / 2
L = m + 1
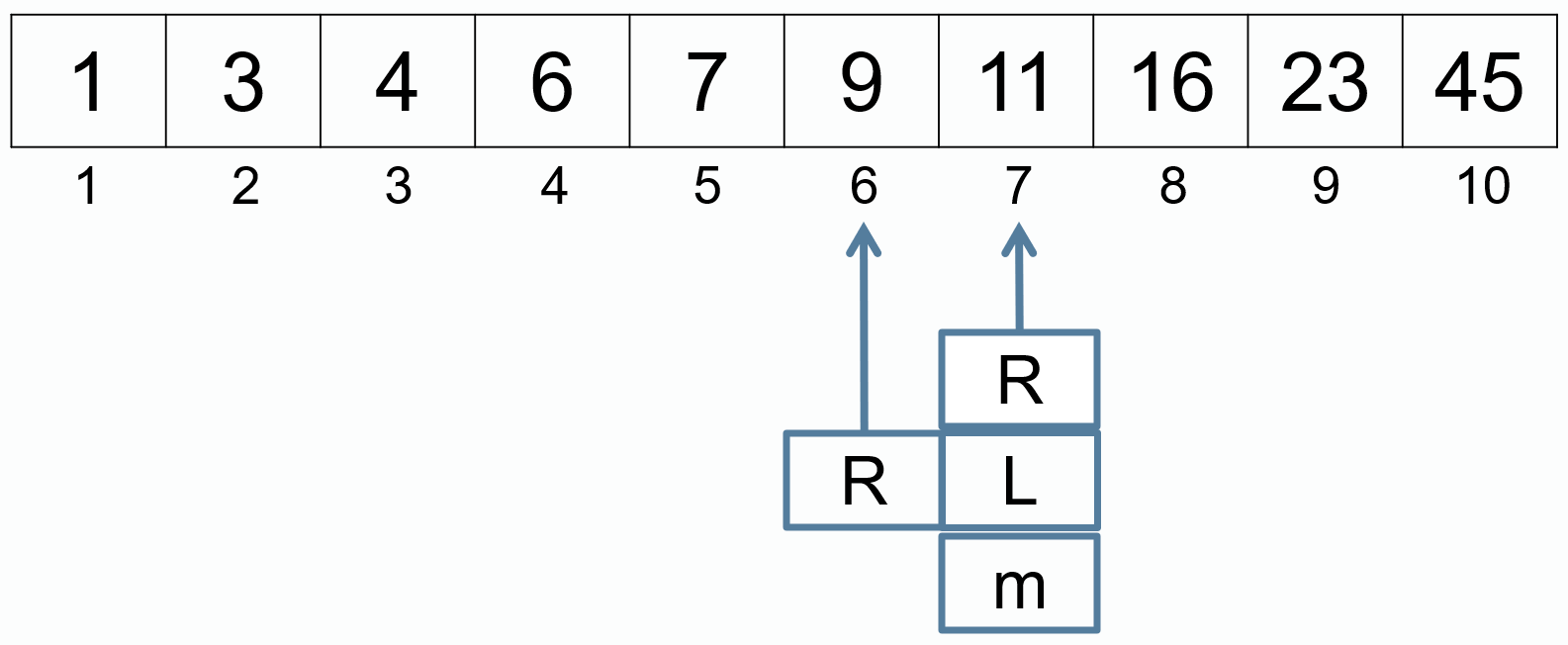
m = (L + R) / 2
R = m - 1
不再满足 L <= R，查找结束，没有找到。
在 n 个元素的有序序列中进行二分查找：
- 最大比较次数：[log2n]+1
- 时间复杂度：O(logn)
二分答案
解题的时候往往会考虑枚举答案然后检验枚举的值是否正确。若满足单调性，则满足使用二分法的条件，把枚举换成二分，就是二分答案。
使用场景：要求我们求出某变量在满足某种条件下的最大值或最小值。
一般看到所谓的最大值最小化或者最小值最大化，通常用二分法就可以很好地解决。
使用前提:
- 答案在一个固定的区间内
- 可能查找一个符合条件的值不是很容易，但给定一个值你可以很快的判断它是不是符合要求
- 可行解对于区间要符合单调性
最小值最大化
//验证答案是否正确
bool check(int x){
//根据具体问题写验证逻辑
}
int main() {
....//输入数据
int l=1,r=n,mid,ans=-1;
while(l<=r){
mid=(l+r)/2;
if(check(mid)){
ans=mid;
l=mid+1;//调整上限，看能不能更大,到后半段去找
}else{
r=mid-1;
}
}
cout<<ans;
return 0;
}
最大值最小化
//验证答案是否正确
bool check(int x){
//根据具体问题写验证逻辑
}
int main() {
....//输入数据
int l=1,r=n,mid,ans=-1;
while(l<=r){
mid=(l+r)/2;
if(check(mid)){
ans=mid;
r=mid-1;//调整下限，看能不能更小,到前半段去找
}else{
l=mid+1;
}
}
cout<<ans;
return 0;
}
快速排序
每一轮挑选一个基准元素（随机选择，编程时一般选取第一个），并让比它大或小的元素移动到基准元素的两边，把数列拆解成了两个部分。而后对这两部分分别进行快速排序。
排序流程
1、首先设定一个分界值，通过该分界值将数组分成左右两部分。
2、将大于或等于分界值的数据集中到数组右边，小于分界值的数据集中到数组的左边。此时，左边部分中各元素都小于或等于分界值，而右边部分中各元素都大于或等于分界值。
3、然后，左边和右边的数据可以独立排序。对于左侧的数组数据，又可以取一个分界值，将该部分数据分成左右两部分，同样在左边放置较小值，右边放置较大值。右侧的数组数据也可以做类似处理。
4、重复上述过程，可以看出，这是一个递归定义。通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后，整个数组的排序也就完成了。
概括来说为 挖坑填数 + 分治法。
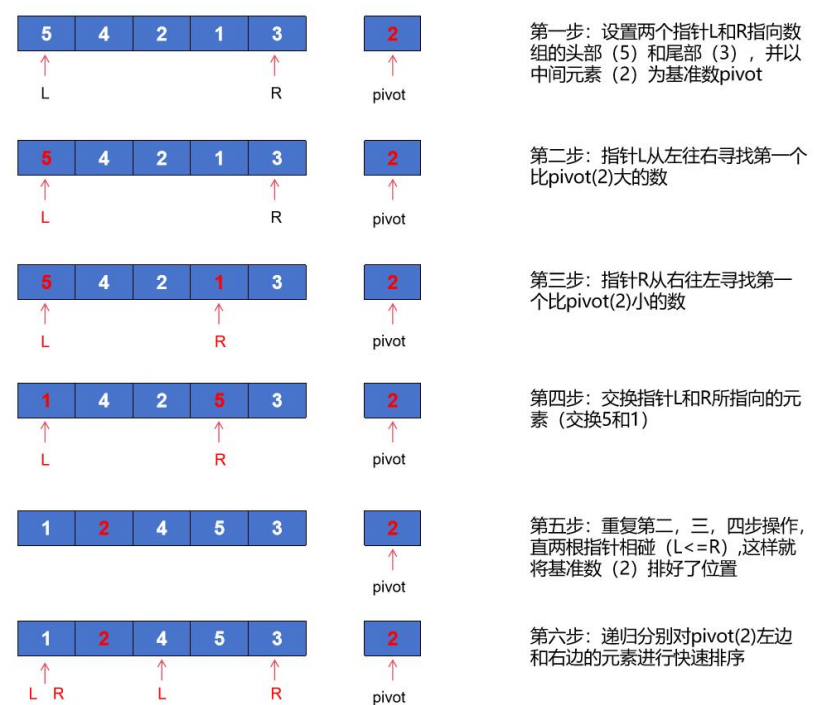
参考代码：
#include<bits/stdc++.h>
using namespace std;
int a[10] = {0, 4, 1, 7, 9, 2, 3, 8, 5, 6};
void quickSort(int start, int end) {
if (start < end) {//数组有多个元素进行排序
int base = a[start];//以要进行排序数组第0个元素为base
int left = start;//左指针
int right = end;//右指针
while (left < right) {
//从右向左找，比base大，right--
while (left< right && a[right] >= base) right--;
//比base小，替换left所在位置的数字
a[left] = a[right];
//从左向右找，比base小，left++
while (left < right && a[left] <= base) left++;
//比base大，替换right所在位置的数字
a[right] = a[left];
}
a[left] = base;//此时left=right，用base替换这个位置的数字
quickSort(start, left - 1);//排列比base小的数字的数组
quickSort(left + 1, end);//排列比base大的数字的数组
}
}
int main(){
quickSort(0, 9);
for(int i = 0; i < 10; i++){
cout << a[i] << ' ';
}
return 0;
}
时间复杂度：
①理想情况下：O(nlogn)。
②最坏情况下：O(N)。
空间复杂度：O(N)
稳定性：不稳定
归并排序
对序列的元素进行逐层折半分组，然后从最小分组开始比较排序，逐层进行合并。
该算法有两个基本的操作，一个是分，也就是把原数组划分成两个子数组的过程；另一个是治，它将两个有序数组合并成一个更大的有序数组。
排序流程
1、将待排序的线性表不断地切分成若干个子表，直到每个子表只包含一个元素，这时，可以认为只包含一个元素的子表是有序表。 2、将子表两两合并，每合并一次，就会产生一个新的且更长的有序表，重复这一步骤，直到最后只剩下一个子表，这个子表就是排好序的线性表。
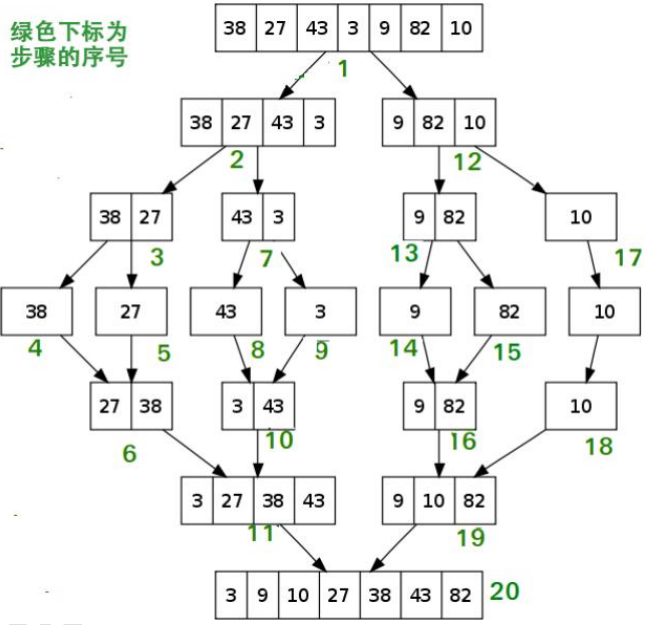
参考代码：
#include<bits/stdc++.h>
using namespace std;
int n,a[10]= {0, 4, 1, 7, 9, 2, 3, 8, 5, 6}, b[10], ans;
void mergeSort(int left,int right) {//排序left到right区间
int mid = (left + right) / 2;
if(left >= right) return;//区间不存在或者只有一个元素 就不排序了
mergeSort(left, mid);//先递归左半部分
mergeSort(mid + 1, right);//再递归右半部分
int l = left, r = mid+1, p = 0;
while(l <= mid && r <= right) {//在合理的区间比较
if(a[l] <= a[r]) {//左边小于右边
b[p++] = a[l++];//存左边
} else {
b[p++] = a[r++];//存右边
}
}
while(l <= mid) b[p++] = a[l++];//特判左区间没有结束，直接全部拷贝到b数组
while(r <= right) b[p++] = a[r++];//特判右区间没有结束，直接全部拷贝到b数组
for(int i = left, p = 0; i <= right; i++,p++) {
a[i] = b[p];//还给a数组(待排原数组)
}
}
int main() {
mergeSort(0,9);
for(int i=0; i<10; i++) {
cout<<a[i]<<' ';
}
return 0;
}
时间复杂度：O(nlogn)。
空间复杂度：O(N)，归并排序需要一个与原数组相同长度的数组做辅助来排序。
稳定性：稳定